Un algorithme glouton (greedy in english) est un algorithme simple et intuitif utilisé dans les problèmes où l'on recherche une solution optimale (problèmes d'optimisation).
Prenons l'exemple ci-dessous correspondant à un problème d'optimisation :
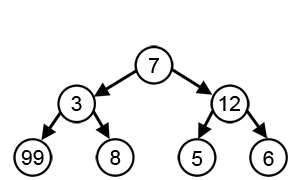
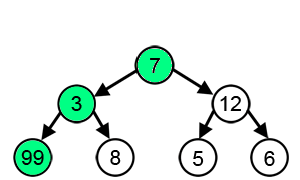
Il s'agit de trouver un chemin partant de la racine de l'arbre et dont la somme des étiquettes est la plus grande possible.
La solution optimale est indiquée ici en vert.
Principe d'un algorithme Glouton.
On utilise ce type d'algorithme lorsqu'on est confronté à un problème d'optimisation pour lequel la recherche de la solution optimale est difficile. En algorithmique, difficile veut dire qu'on ne peut pas résoudre le problème en un temps raisonnable. Habituellement cela veut dire que la complexité est plus que polynomiale. Pour pouvoir utiliser un algorithme glouton, il faut qu'on puisse fournir de multiples solutions, certaines optimales, certaines bonnes et d'autres plutôt mauvaises. S'il n'y a qu'une solution UNIQUE, ce n'est pas de l'optimisation !
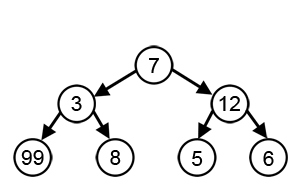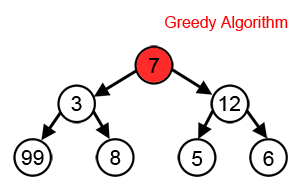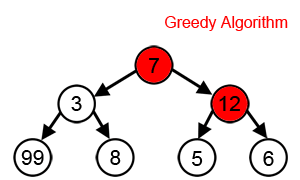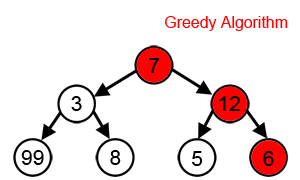
Dans le cas de la recherche de notre chemin dans un arbre, l'algorithme glouton sélectionne le plus grand nombre disponible à chaque étape.
Notons que le terme anglais "greedy" se traduit également par cupide, avide, qui illustre bien l'idée de cet algorithme qui est de choisir la grande valeur possible à chaque étape.
Limites de l'algorithme.
Cependant, comme nous pouvons le voir dans l'animation ci-dessous, cette approche ne parvient toujours pas à trouver la somme la plus élevée, En effet l'algorithme prend des décisions uniquement en fonction des informations dont il dispose à chaque étape, sans tenir compte du problème global.
Notons, que les algorithmes Gloutons réussissent assez bien dans certains problèmes, tels que l' encodage de Huffman, utilisé pour compresser les données, ou l'algorithme de Dijkstra , qui permet de trouver le chemin le plus court dans un graphe.
Quoiqu'il en soit, même si la stratégie gourmande ne produit pas toujours une solution optimale, elle permet de proposer une solution.
C'est le cas par exemple dans le problème dit "du sac à dos" et dans le problème dit "du rendu de monnaie" que nous allons étudier.
Le problème du sac à dos.
Pour info, le problème du sac à dos est l'un des 21 problèmes NP-complets de Richard Karp, exposés dans un article de 1972. La formulation du problème est fort simple, mais sa résolution est plus complexe.

Le problème consiste à remplir un sac à dos, ne pouvant supporter plus d'une certaine masse, avec tout ou partie d'un ensemble donné d'objets ayant chacun une masse et une valeur. Les objets mis dans le sac à dos doivent maximiser la valeur totale, sans dépasser la masse maximum.
Algorithme

Une astuce consiste à trier les objets dans l'ordre décroissant de leur valeur.
Un cambrioleur possède un sac à dos d'une contenance maximum de 30 Kg. Au cours d'un de ses cambriolages, il a la possibilité de dérober 4 objets A, B, C et D. Voici un tableau qui résume les caractéristiques de ces objets :
| objet | A | B | C | D |
|---|---|---|---|---|
| masse | 13 Kg | 12 Kg | 8 Kg | 10 Kg |
| valeur marchande | 700 € | 400 € | 300 € | 300 € |
Ce genre de problème est un grand classique en informatique, on parle de problème d'optimisation. Il existe toujours plusieurs solutions possibles à un problème d'optimisation (dans le problème du sac à dos, on peut choisir A+B ou A+C ou B+C+D... toutes les combinaisons sont possibles à partir du moment où la masse totale ne dépasse pas 30 Kg), mais on ne cherche pas n'importe quelle solution, on cherche une solution dite optimale : dans notre exemple on cherche le plus grand gain possible. Souvent, dans les problèmes d'optimisation, il n'existe pas une solution optimale, mais plusieurs solutions optimales, résoudre un problème d'optimisation c'est donc trouver une des solutions optimales.
Il existe différentes méthodes algorithmiques permettant de trouver une solution optimale à un problème d'optimisation : il peut, en effet, être intéressant "d'automatiser" la résolution des problèmes d'optimisation à l'aide d'algorithme (dans notre cas, trouver un algorithme qui trouve une solution optimale au problème du sac à doc).
En apparence, la solution la plus simple dans le cas du sac à dos serait d'écrire un algorithme qui teste toutes les combinaisons d'objets possibles et qui retient les solutions qui offrent un gain maximum. Dans notre cas précis, avec seulement 4 objets, cette solution pourrait être envisagée, mais avec un plus grand nombre d'objets, le temps de calculs, même pour un ordinateur très puissant, deviendrait trop important. En effet l'algorithme qui testerait toutes les combinaisons possibles aurait une complexité en temps en O(an) avec a une constante et n les nombre d'objets. On parle d'une complexité exponentielle. Les algorithmes à complexité exponentielle ne sont pas efficaces pour résoudre des problèmes, le temps de calcul devient beaucoup trop important quand n devient très grand.
À la place de cette méthode "je teste toutes les possibilités", il est possible d'utiliser une méthode dite gloutonne (greedy en anglais).
-
Sachant que l'on cherche à maximiser le gain, commençons par établir un tableau nous donnant la "valeur massique" de chaque objet (pour chaque objet on divise sa valeur par sa masse) :
valeur massique des objets objet A B C D valeur massique 54 €/Kg 33 €/Kg 38 €/Kg 30 €/Kg
- On classe ensuite les objets par ordre décroissant de valeur massique : A - C - B -D
-
Enfin, on remplit le sac en prenant les objets dans l'ordre et en s'arrêtant dès que la
masse limite est atteinte. C'est ici que ce fait "le choix glouton", à chaque étape, on
prend l'objet
ayant le rapport "valeur-masse" le plus intéressant au vu des objectifs :
- 1re étape : A (13 Kg)
- 2e étape : C (13+8=21 Kg)
- 3e étape : B (13+8+12=33 Kg) => impossible, on dépasse les 30 Kg.
Le sac est donc composé de 2 objets : A et C pour un montant total de 1000 € et une masse totale de 21 Kg.
Cette méthode gloutonne peut être "automatisée", il est donc possible d'écrire un algorithme glouton (un algorithme qui est basé sur une méthode gloutonne) afin de trouver une solution au problème du sac à dos avec n'importe quelles valeurs (nombre d'objets, masse des objets, valeur des objets, masse maximum).
La solution trouvée ci-dessus est-elle optimale ?
On constate rapidement que la réponse est non, car le couple A+B permet d'atteindre une valeur de 1100 € pour une masse de 25 Kg. Dans notre problème, la méthode gloutonne ne nous donne pas une solution optimale.
Plus généralement , il est important de bien comprendre qu'un algorithme glouton ne donne pas forcement une solution optimale. Pour certains types de problèmes, il est possible de démontrer qu'un algorithme glouton donnera toujours une solution optimale, mais cela dépasse largement le cadre de ce cours.
Plutôt que de trier les objets par valeurs décroissantes, on peut aussi travailler avec le ratio valeur/Masse.
on tente une nouvelle formule pour les exos :-)
pour ça, rendez vous ici
Rendu de monnaie
Autre problème typique : le rendu de monnaie.
Imaginons une somme de 5,50 euros à rendre.
Nous avons à disposition le billet de 5 euros, la pièce de 2 euros, la pièce de 1 euro, la pièce de 50 cents, la pièce de 20 cents, la pièce de 10 cents, la pièce de 5 cents.
Pour le transformer en problème d'optimisation, il faut rajouter une condition : on veut une solution pour laquelle on rend le moins de pièces ou de billets possibles.
Pour un humain, ça ne pose pas de problème : un billet de 5 euros et une pièce de 50 cents.
Mais vous vous rendez bien compte des possibilités possibles à comparer pour une machine...
Nous allons donc appliquer une stratégie gloutonne en choisissant cette solution locale optimale : toujours compléter la somme à rendre avec le billet ou la pièce la plus grande utilisable.
En appliquant ce principe, que doit-on donner si on doit rendre 29 euros à l'aide de billets de 20 euros, 10 euros et 5 euros et de pièces de 2 euros et 1 euro ?
Fournir la réponse de notre stratégie gloutonne si on doit rendre 10 euros en choisissant dans l'ensemble { 5, 2, 1 }. Est-ce la solution optimale pour notre ensemble de pièces disponibles ?
Fournir la réponse de notre stratégie gloutonne si on doit rendre 10 euros avec l'ensemble { 8, 5, 1 }. Proposer une meilleure solution en utilisant votre cerveau et pas la stratégie gloutonne.
Et voilà. Ca fonctionne toujours pourvu qu'on ai une pièce correspondant à la plus petite somme à rendre mais ça ne donne pas toujours la solution optimale. De toutes manières, évaluer toutes les possibilités ne devrait pas faire diminuer significativement le nombre de pièces à rendre.
Rendu de monnaie avec Python
Nous allons finir en appliquant la stratégie gloutonne du rendu de monnaie à Python.
On commencera par créer un tableau les_choix regroupant les sommes qu'on peut rendre et une fonction rendre qui récupère la somme à rendre dans le paramètre a_rendre et le tableau des billets et pièces disponible dans le paramètre choix.
Cette fonction devra renvoyer un tableau contenant les éléments à rendre. Par exemple
[100, 10, 5, 2, 2] pour rendre 119 euros.
les_choix = [100, 50, 20, 10, 5, 2, 1]
def rendre(a_rendre, choix=les_choix):
reponse = []
return reponse
On remarquera que le deuxième paramètre de la fonction, choix possède une valeur par défaut : nous ne sommes pas obligés de lui transmettre ce tableau. Si on ne lui transmet rien, il va alors remplir ce paramètre avec la variable les_choix.
On pourra donc activer l'appel de notre fonction simplement de cette façon pour rendre 12 euros :
>>> rendre(12)
Mais on pourra également fournir une valeur pour le paramètre choix :
>>> rendre(12, [50, 20, 10, 1])
>>> rendre(12, les_choix)
Voici l'algorithme que vous allez devoir créer en Python :
Algorithme glouton du rendu de monnaie
Description des entrées / sortie
ENTREES:a_rendre: la somme à rendre.choix: un tableau trié en ordre décroissant contenant l'ensemble des billets ou pièces permettant de rendre la monnaie. Votre tableau doit contenir une valeur finale permettant de rendre la plus petite somme possible.- (optionnelle selon les langages d'implémentation):
longueur, le nombre d'éléments dans le tableau SORTIE: un tableau contenant les éléments (billets ou pièces) à rendre.
Algorithme commenté
reponse ← []
ce tableau vide initialement va contenir la réponse
reste ← a_rendre
reste va contenir ce qu'on doit encore rendre, au départ elle contient donc a_rendre
index ← 0
on va commencer par le premier élément fourni dans choix, l'élément de plus grande valeur
TANT QUE
reste est strictement supérieure
0
SI
reste est supérieure ou
égale à
choix[index]
on peut rendre une partie de l'argent avec le billet ou la pièce choix[index]
reste ← reste -
choix[index]
on rajoute
choix[index]
dans reponse
SINON
choix[index] est plus grand que la somme à rendre, il faut passer au billet ou la pièce suivante
index ← index +
1
Fin Si
Fin Tant que
Si on arrive ici, c'est qu'on est sorti du tant que : reste valait 0
Renvoyer reponse
Compléter la fonction Python ci-dessous (en modifiant les ...) pour qu'elle applique correctement l'algorithme ci-dessus.
les_choix = [100, 50, 20, 10, 5, 2, 1]
def rendre(a_rendre, choix=les_choix):
reponse = []
reste = a_rendre
index = 0
while ... :
if ... :
....
....
else :
...
return reponse
Vous trouverez ci-dessous quelques indications vous permettant d'avancer.
Rappel : pour rajouter à élément à un tableau, il faut utiliser la méthode append.
>>> fruits = ['Ananas']
>>> fruits.append('Banane')
>>> fruits
['Ananas', 'Banane']
Avertissement : je ne veux voir que choix dans le corps de votre fonction. N'utilisez pas la variable globale mes_choix. Elle sert uniquement de valeur par défaut au paramètre choix.
Exemple de résultats attendus (je n'ai pas mis de doctest, car vous aurez à le faire dans quelques questions) :
>>> rendre(15)
[10, 5]
>>> rendre(17)
[10, 5, 2]
Analysons un peu le programme réalisé.
En apparence, puisque la condition du TANT QUE est une condition du type
while un > 0
et que reste va décroître, on pourrait croire qu'elle se
termine bien à tous les cas. Erreur.
Répondre aux trois questions suivantes qui traitent des erreurs d'exécution possibles.
Question 1 : Le programme pourrait-il fonctionner
avec des euros entiers si nous avions le tableau suivant (dans lequel il manque
juste la pièce d'un euro) :
les_choix = [100, 50, 20, 10, 5, 2]) ?
Faire le test avec
rendre(13) et
rendre(12)
pour tenter de voir s'il peut tourner en boucle.
Question 2 : Que va-t-il se
passer si on demande
rendre(17.5) ?
Que pourrait-on faire pour permettre au système de gérer les centimes ?
Question 3 : Le programme
pourrait-il fonctionner avec des cents (en rajoutant les cents dans le tableau bien
entendu :
les_choix = [100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.02, 0.01]) ?
Faire le test avec
rendre(17.50)
et
rendre(17.15)
pour tenter de voir s'il peut tourner à chaque fois.
Float
L'encodage des floats est approximatifs dans la plupart des cas.
Il faut donc être très vigilant à leur propos.
- JAMAIS DE TEST D'EGALITE ENTRE DEUX FLOAT !
- VIGILANCE SUR LES CALCULS REPETIFS
>>> 0.3 == (3*0.1)
False
a = 0.1
b = 0.3
c = b - 3*a
for d in range(1000):
c = c*2
print(c)
Alors qu'on devrait afficher 0, c contient -5.948.10284 !
Comment faire alors pour traiter les cents ? Le plus "simple" est d'arrondir les calculs à chaque fois. Dans la solution que je vous propose, j'utilise la fonction native round qui permet d'arrondir au plus proche et en précisant le nombre de chiffres après la virgule à gérer. Ici, j'en place 2, par arrondir correctement au centime. 14.009999 euros va donc devenir 14.01 et nous éviterons le problème précédent.
les_choix = [100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.01]
def rendre(a_rendre, choix=les_choix):
reponse = []
reste = round(a_rendre, 2)
index = 0
while reste > 0 :
if reste >= choix[index] :
reste = round(reste - choix[index], 2)
reponse.append(choix[index])
else :
index = index + 1
return reponse
Tester la fonction avec deux trois valeurs pour vous persuader que cela fonctionne bien maintenant avec les centimes.
Une méthode plus propre consisterait plutôt à ne faire travailler la fonction qu'avec des cents. Comme cela, les calculs sont faits avec des entiers. Plus de problème de résultats approximatifs à cause de l'encodage des flottants.
0.1 euro est donc transformé en 10 cents.
5 euros est transformé en 500 cents...
Utiliser le programme puis répondre aux questions.
les_choix = [100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.01]
def rendre(a_rendre, choix=les_choix):
choix_en_cents = [round(valeur*100) for valeur in choix]
reponse = []
reste = round(a_rendre*100)
index = 0
while reste > 0 :
if reste >= choix_en_cents[index] :
reste = reste - choix_en_cents[index]
reponse.append(choix[index])
else :
index = index + 1
return reponse
Question 1 : donner le contenu du tableau choix_en_cents après exécution de la ligne 4. Tenir compte du tableau fourni en ligne 1.
Question 2 : comment se nomme cette manière de créer un tableau : par compréhension, par extension et ajouts successifs, par omission, par dissimulation ?
Question 3 : les calculs des lignes 9 et 10 sont donc faits en cents. En regardant la ligne 10, dire si le résultat transmis par la fonction va lui être donné en euros ou en cents ?
Voilà pour le petit détour pour le problème des flottants. Comme vous le constatez, même avec un algorithme plutôt facile, il vaut toujours veiller aux calculs lorsqu'ils intègrent possiblement des nombres à virgules.
Ecrire la documentation de la fonction :
- phrase rapide d'explication,
- préconditions (sur les paramètres d'entrée),
- la ou les post-conditions (sur la réponse)
- au moins un exemple permettant de comprendre son fonctionnement et de l'utiliser éventuellement pour un doctest.
Vous noterez que j'ai rajouté ici une assertion pour provoquer une exception/erreur lorsqu'on demande de rembourser une somme négative. Pensez à en tenir compte lors de la rédaction de la documentation : la fonction n'accepte pas de valeurs négatives à rembourser.
les_choix = [100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.01]
def rendre(a_rendre, choix=les_choix):
assert a_rendre > 0, "La somme à rendre doit être positive ou nulle à la limite"
choix_en_cents = [round(valeur*100) for valeur in choix]
reponse = []
reste = round(a_rendre*100)
index = 0
while reste > 0 :
if reste >= choix_en_cents[index] :
reste = reste - choix_en_cents[index]
reponse.append(choix[index])
else :
index = index + 1
return reponse
Nous en avons fini avec cette présentation des algorithmes gloutons.
Stratégie gloutonne
La stratégie gloutonne est une stratégie de résolution de problèmes complexes, liée à l'optimisation d'une solution : il faut qu'il y ai plusieurs solutions possibles.
La stratégie gloutonne consiste à
- faire des choix locaux qu'on pense efficaces
- pour résoudre le problème au niveau global.
On ne regarde pas au loin pour avoir une idée globale de la solution, chaque décision est prise en fonction des contraintes locales au moment du choix à faire.
Quelques exemples de problèmes et de solutions locales associées que nous avons vu :
- Sac à dos: on maximise le poids du sac
- Rendu de monnaie : on choisit le billet ou la pièce la plus grosse encore utilisable