Algorithme
Histoire
On peut donner différentes définition d'un algorithme en voila une :
Algorithme
Un algorithme est une suite
d’instructions élémentaires appliquées dans un ordre déterminé portant sur un
nombre fini de données pour arriver, en un nombre fini d'étapes, à un certain résultat.
Quelques repères historiques :
Les premiers algorithmes ont été développés bien avant l'émergence de l'informatique et même bien avant le
grand savant Muhammad ibn Musa al-Khwârizmî
dont le nom latinisé a donné le mot algorithme.
De plus, vous manipulez des algorithmes depuis votre prime enfance : une recette de cuisine est un exemple
concret d'algorithme !
Vers -1800 :
Les plus anciens algorithmes connus remontent il y a presque quatre millénaires.
Les
Babyloniens
qui vivaient en Mésopotamie (actuel Irak) utilisaient des algorithmes
pour résoudre certaines équations (comme celles du second degré).
Voici l'image d'une tablette datant de cette période où plusieurs problèmes du second degré sont résolus par
une sorte de liste
d'instructions proche de nos algorithmes actuels :

Vers -300 :
Euclide a proposé entre autre un algorithme, encore utilisé de nos jours, permettant le plus grand
commun diviseur (le PGCD)
entre deux nombres entiers. Vous avez vu cet algorithme d'Euclide au collège.
Voici une illustration de cet algorithme :

Vers 800 :
Le mot algorithme vient du nom latinisé du grand mathématicien Al-Khwârizmî .
/Al-Khwarizmi-head-5693a8955f9b58eba491f07c.jpg)
Ce savant ayant vécu entre 780 et 850 fut membre de la Maison de la Sagesse de Bagdad. Il répertoria les
algorithmes connus à son époque
et, entre autres travaux, il fut l’auteur entre autre de deux livres importants :
- le premier a conduit au mot « algèbre » actuel ;
- le second a permis la diffusion du système de numération décimal actuel à travers le monde abbasside
puis en Europe : ce sont les « chiffres arabes » actuels.
XVII siècle :
Afin de réduire le temps de calcul et surtout les risques d'erreurs de calcul, à partir du XVII sicèle, des
calculateurs mécaniques ont été construits.
Voici l'image de la toute première calculatrice construite par Blaise Pascal en 1645 capable d'effectuer des
additions et des soustractions :
la Pascaline .

XIX siècle :
Exaspéré par les nombreuses erreurs présentes dans les tables utilisées pour faire des calculs compliqués en
sciences (astronomie, physique, ...),
l'anglais Charles Babbage conçoit les plans d'une machine capable de calculer puis d'éditer les valeurs de
fonctions polynomiales.
Ada Lovelace, la fille du poète Lord Byron, travaille un temps avec Charles Baggage et écrit en 1843 le
premier algorithme exécutable sur une machine : c'est le premier programme informatique !

1936 :
Le concept de machine universelle, capable d’exécuter tous les algorithmes est développé par Alan
Turing. Les notions de machine, d'algorithme, de langage et d'information sont pensées
désormais comme un tout cohérent.
1943 :
La première machine électronique, le Colossus, a été construite en 1943 en Angleterre et a été
utilisé pour décrypter les codes secrets allemands fondés sur la machine Enigma.
1948 :
Le premier ordinateur suivant l'architecture de Von Neumann est construite aux États-Unis. C'étaient
surtout des femmes qui travaillaient dans la programmation
des premiers ordinateurs.
Le seul langage directement utilisable par le processeur des ordinateurs est le langage machine (abordé
brièvement plus tard dans cette année).
Pour faciliter la communication d'informations avec un ordinateur, des informaticiens ont créé des
langages dits de haut niveau qui sont plus simples
à utiliser, car plus proches du langage naturel.
Il y en a un très grand nombre (FORTRAN (1955), C (1972), PHP (1994), JAVA (1995), Javascript (1995), ... )
Celui que vous utiliserez énormément cette année est le langage PYTHON, créé en 1991 par Guido Von Rossum.
Pseudo-code
Puisqu'il y a un très grand nombre de langages différents, il est commode d'utiliser une sorte de lingua
franca qui permet d'écrire un algorithme
dans un langage "universel". Le pseudo-code sert à cela !
Le pseudo-code est un langage pour exprimer clairement et formellement un algorithme.
Ce langage est près d'un langage de programmation comme Pascal, C# ou C++, sans être identique à l'un ou à
l'autre.
Il exprime des idées formelles dans une langue près du langage naturel de ses usagers (pour nous, le
français) en lui imposant une forme rigoureuse.
Il n'y a pas de standard normalisé mais seulement des conventions partagées par un plus grand nombre de
programmeurs.
Quelques règles :
- Le nom d'un variable ou d'une constante doit être significatif. On devrait savoir immédiatement, à
partir de son nom, à quoi sert la variable ou la constante, et quel sens donner à sa valeur
- Les majuscules et les minuscules sont des symboles distincts dans la plupart des langages de
programmation, mais pas tous.
Ainsi, pour éviter les ennuis, ne donnez pas à deux entités (une variable et une constante, par
exemple)
des noms qui ne différeraient que sur cet aspect
- Les instructions se font une ligne à la fois (pas de ';' en pseudo-code)
- On ne se préoccupe pas des types des variables et des constantes (ce principe n'est pas universel)
- Les opérations de base sont LIRE, ÉCRIRE et ← (affectation d'une valeur à une variable). Les
opérations
de base et/ou mots clés doivent être écrits en gras ou en majuscules
Réaliser l'exercice dans le dépôt
Les variables
A quoi servent les variables ?
Dans un programme informatique, on va avoir en permanence besoin de stocker provisoirement des valeurs.
Il peut s’agir de données issues du disque dur, fournies par l’utilisateur (frappées au clavier), ou que
sais-je encore. Il peut aussi s’agir de résultats obtenus par le programme, intermédiaires ou définitifs.
Ces données peuvent être de plusieurs types (on en reparlera) : elles peuvent être
des
nombres, du texte,
etc.
Toujours est-il que dès que l’on a besoin de stocker une information au cours d’un programme, on utilise une
variable.
Pour employer une image, une variable est une boîte, que le programme (l’ordinateur) va repérer par une
étiquette.
Pour avoir accès au contenu de la boîte, il suffit de la désigner par son étiquette.
Ainsi, ci-dessous la variable x est l'étiquette d'une boîte contenant l'entier 5.
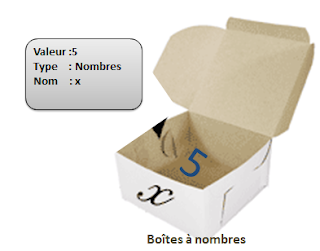
En réalité, dans la mémoire vive de l’ordinateur, il n’y a bien sûr pas une vraie boîte, et pas davantage de
vraie étiquette collée dessus (j’avais bien prévenu que la boîte et l’étiquette, c’était une image).
Dans l’ordinateur, physiquement, il y a un emplacement de mémoire, repéré par une adresse binaire. Si on
programmait dans un langage directement compréhensible par la machine, on devrait se fader de désigner nos
données par de superbes 0010 (souvent écrit en héxadécimal 0002) ou 10011011 (enchanté !).
Ainsi ci-dessous, la variable nommée x fait référence à l'emplacement de mémoire dont l'adresse en
hexadécimale est 0002.
Cet emplacement mémoire stocke le nombre 5.

Mauvaise nouvelle : de tels langages existent ! Ils portent le doux nom d’assembleur.
Bonne nouvelle
: ce ne
sont pas les seuls langages disponibles.
Les langages informatiques plus évolués (ce sont ceux que presque tout le monde emploie) se chargent
précisément, entre autres rôles, d’épargner au programmeur la gestion fastidieuse des emplacements mémoire
et de leurs adresses.
Et, comme vous commencez à le comprendre, il est beaucoup plus facile d’employer les étiquettes de son
choix, que de devoir manier des adresses binaires.
Déclaration des variables et affectations
Il existe de nombreux types de variables utilisés :
| types |
Remarques |
| booléen |
vrai ou faux |
| caractère |
symboles typographiques |
| chaine de caractères |
ensemble de caractères entre " " |
| entier |
entiers relatifs |
| flottant |
"Utilisé pour les réels" |
Il existe d'autres types de variables. Le fait de déclarer en pseudo-code le type de la variable n'est pas
une obligation, mais vous le verrez dans de nombreux sites car de nombreux langages de programmation
nécessitent un typage strict.
Le langage PYTHON est auto-typé, c'est-à-dire le typage se fait lors de l'affectation.
Comme vu précédemment, en pseudo-code, l'instruction d'affectation se note avec le signe ←
1 toto ← 40
On attribue la valeur 40 à la variable toto
Les instructions
Test IF THEN ELSE
Cette instruction conditionnelle teste une expression booléenne (condition après le if) et exécute soit un bloc
d'instruction(s) si la
condition est vraie (bloc 1 après le then) soit un éventuel autre bloc d'instruction(s) si la
condition est fausse (bloc 2 après le else)
1 if condition then
2 bloc 1
3 else
4 bloc 2
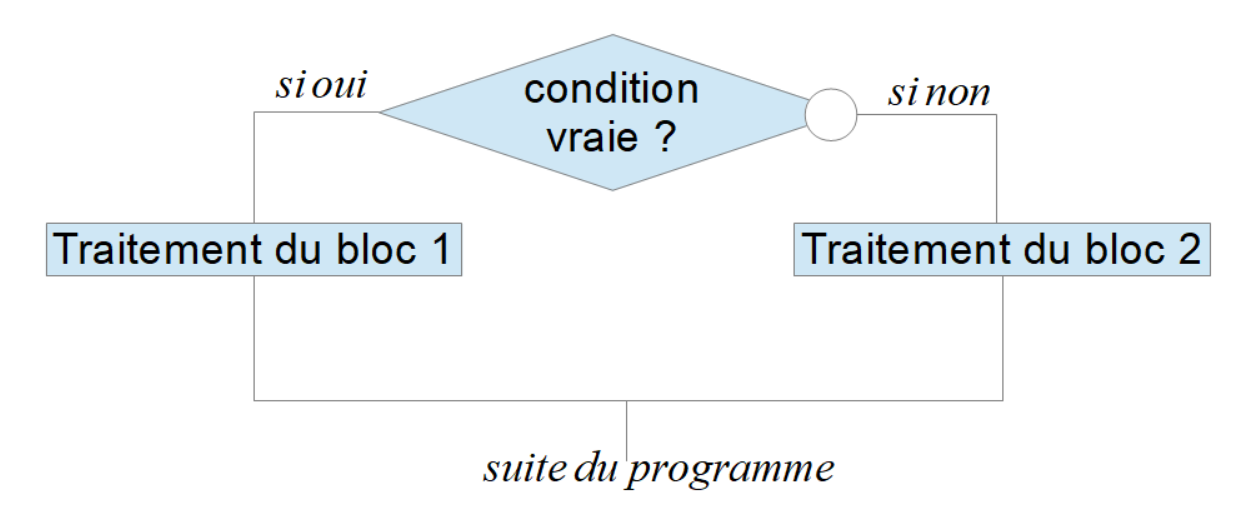
Voici une manière imagée de visualiser cette instruction :

- La partie else n'est pas obligatoire. On peut utiliser l'instruction if ...then,
- Il existe de nombreuses variantes pour indiquer les blocs d'instructions:
Vous pouvez pratiquer du pseudo-code en français ou utiliser l'anglais (il faut vous habituer à lire du
pseudo-code en anglais).
Une version francisée avec une identification des blocs différentes pourraient être :
1 si condition alors
2 bloc 1
3 sinon
4 bloc 2
Une autre manière de visualiser cette instruction, sous forme d'algorigramme :
Voici un algorithme affichant le signe d'un nombre a saisi par l'utilisateur :
1 LIRE a
2 if a>0 then
3 ÉCRIRE "a positif"
4 else
5 ÉCRIRE "a négatif"
Boucle FOR
L'instruction Pour est utilisée lorsque le nombre d'itérations est connu à l'avance : elle
initialise un
compteur, l'incrémente (c'est-à-dore l'augmente de 1) après chaque exécution du
bloc d'instructions,
et vérifie que le compteur ne dépasse pas la borne supérieure.
1 for compteur←entier1 to entier2
2 bloc d'instructions
On peut préciser le pas d'incrémentation du compteur. Par défaut le pas est de 1. Le mot clé en
anglais pour
le pas est le mot STEP.
Voici une illustration de l'algorithme suivant :
1 for i←1 to 4
2 bloc d'instructions

Voici un algorithme affichant les 10 premiers nombres entiers : ceux de 0 à 9 :
1 for i←0 to 9
2 ÉCRIRE i
Boucle WHILE
L'instruction While est utilisée lorsque le nombre d'itérations n'est connu à l'avance : elle répète
l'exécution le bloc d'instructions tant que la condition est vraie.
1 while condition vraie
2 bloc d'instructions
Une manière de visualiser cette instruction, sous forme d'algorigramme :
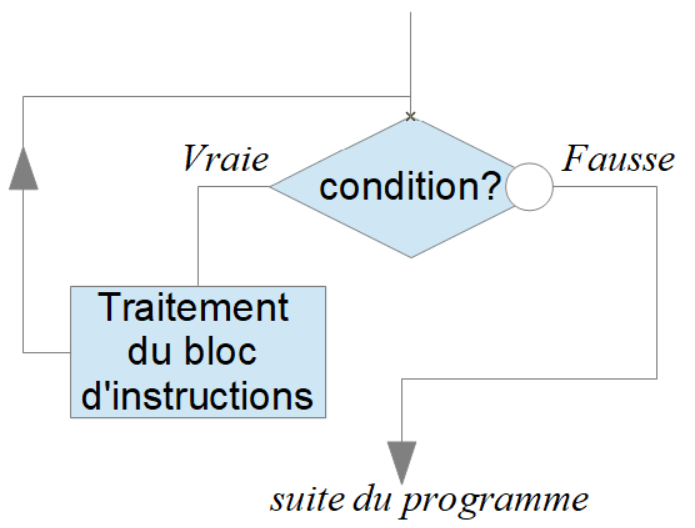
Voici un algorithme affichant tous les carrés inférieurs à 50 :
1 i ← 0
2 while i*i < 50
3 ÉCRIRE i*i
4 i ← i+1
-
Faire attention à éviter une boucle infinie !
-
Dans l'exemple précédent l'incrémentation de i assure la fin de la boucle WHILE.
-
De plus, si la condition n'est pas vraie initialement, aucune itération de la boucle WHILE n'a lieu.
L'importance des commentaires
Il faut prendre l'habitude de commenter ses algorithmes et ses programmes.
- cela permet une relecture facile du code
- cela permet une lecture plus facile pour une personne tierce (un correcteur par exemple)
- commenter n'est pas paraphraser. Le commentaire doit apporter une information
Voici l'algorithme sans les commentaires :
1 n←O
2 p←50
3 while p<100
4 p←p*1.1
5 n←n+1
6 ÉCRIRE n
Il existe différentes façons de noter un commentaire : //, #,
<- ->
Voici l'algorithme avec les commentaires :
// Cet algorithme cherche la valeur de n pour que p passe de 50 à 100 avec une augmentation de 10%
1 n←O //Initialisation de n
2 p←50 //Initialisation de p
3 while p<100
4 p←p*1.1 //p suivie de 10 % d'augmentation
5 n←n+1 //Incrémentation de n
6 ÉCRIRE n
Avec trop de commentaires, le code devient illisible. Sans commentaire, le code est
incompréhensible. A vous de trouver le juste milieu.
Réaliser l'exercice dans le dépôt
Table d'éxécution d'un algorithme
Il existe différentes manières de réaliser une trace de programme et/ou d'algorithme. Une
trace :
- permet de suivre pas à pas l'algorithme;
- permet de détecter des erreurs;
- permet de contrôler que l'algorithme fait bien ce que l'on avant prévu;
- permet de comprendre ce que fait un algorithme.
Dans la mesure du possible, on peut organiser une trace d'exécution d'un
algorithme en constituant un tableau
avec toutes les variables de l'algorithme. Il faut numéroter toutes les lignes de votre
algorithme.
En colonne, il faut indiquer le nom des variables et en ligne les numéros de ligne.
En Python, nous pourrons étudier chaque étape d'un programme grâce à Python tutor ou directement dans l'explorateur de variables.
r←0
while r*r<= n
r←r+1
r←r-1
Il faut commencer par numéroter toutes les lignes de l'algorithme.
1 r←0
2 while r*r<= n
3 r←r+1
4 r←r-1
Voici une trace de l'algorithme avec n=5. quelle est la valeur de la variable r ?
| #ligne |
n |
r |
Commentaires |
| 1 |
5 |
0 |
Initialisation |
| 2 |
5 |
0 |
0*0<=5 , on entre dans la ligne 3 |
| 3 |
5 |
1 |
r←1 |
| 2 |
5 |
1 |
1*1<=5 , on entre dans la ligne 3 |
| 3 |
5 |
2 |
r←2 |
| 2 |
5 |
2 |
2*2<=5 , on entre dans la ligne 3 |
| 3 |
5 |
3 |
r←3 |
| 2 |
5
| 3 |
3*3>5 , on sort de la boucle |
| 4 |
5 |
2 |
r←2 |
À la fin de l'algorithme, la variable r a pour valeur 2
En mathématiques, vous auriez une version minimaliste de ce tableau, qui correspondrait à
l'état des variables :
| n |
5 |
5 |
5 |
5 |
5 |
5 |
| r |
0 |
0 |
1 |
2 |
3 |
2 |
Nous allons favoriser des traces de ce type :

Exercices
Réaliser la série d'exercice du dépôt
Prolongements
Il existe un mode de représentation des algorithmes sous forme d'organigrammes : Les
algorigrammes
Vous pouvez vous rendre à l'adresse suivante : https://troumad.developpez.com/C/algorigrammes/
Il existe des logiciels permettant de réaliser des organigrammes (lucidchart, word, paint,
etc)
Un exemple avec le site lucidchart
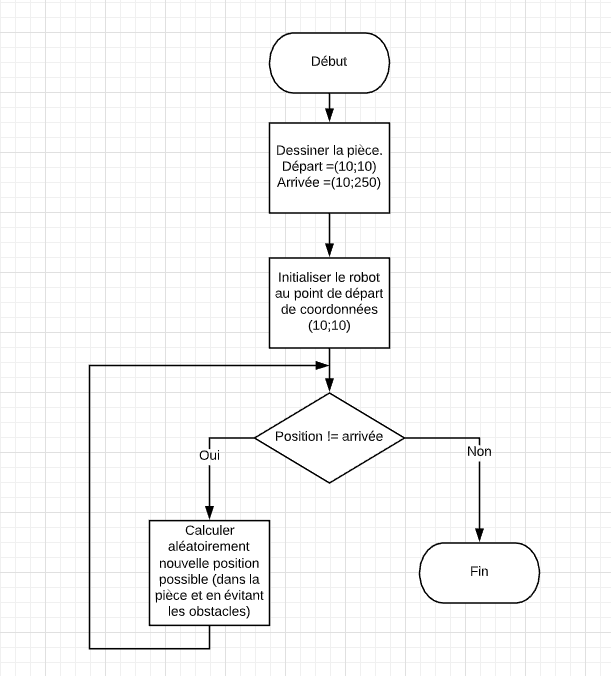
Vous pouvez réaliser un algorigramme d'un algorithme que vous avez traité dans le TD
Savoir faire et Savoir
- Écrire un algorithme simple
- Réaliser la trace d'un algorithme
- Les types de variables
- Écrire une affection
- Écrire un test conditionnel si
- Écrire une boucle itérative pour
- Écrire une boucle itérative tant que