Recherche dans une liste, l'algorithme naïf
Pour trouver un nombre dans une liste il suffit de balayer la liste et de renvoyer True dès qu’on trouve l’élément recherché et False si on a parcouru toute la liste sans trouver l’élément.
//déclarations val: Valeur cherchée (entier) i: Entier liste : liste de N entiers triés retour : Booléen //initialisation retour ← faux i ← 0 //Boucle de recherche // La condition début inférieur ou égal à fin permet d'éviter de faire // une boucle infinie si 'val' n'existe pas dans le tableau. Tant que i <= N et retour est faux: si liste[i] == val: retour ← vrai i ← i+1 //Affichage du résultat Si retour == vrai: Afficher "La valeur ", val , " est dans la liste." Sinon: Afficher "La valeur ", val , " n'est pas dans la liste."
Implémentez la recherche d'un élément dans une liste triée en Python.
Puis tester les valeurs 3 et 4 avec la liste: ma_liste=[3,5,12,15,48]
On voit que cet algorithme n'est peut-être pas le plus pertinent, car dans le pire des cas, c'est à dire le cas ou l'élément cherché n'est pas présent, on devra parcourir toute la liste.
La dichotomie: généralités
Cette méthode, vous la connaissez tous!
Vous avez probablement joué au jeu :trouve un nombre entre 1 et 100. Vous avez commencé par proposer 50. Si on vous répond, c'est plus, vous proposez 75 puis si l'on vous répond c'est moins vous proposez 62... Vous êtes alors en train d'effectuer une recherche dichotomique !
Faire une recherche dichotomique, c'est chercher une valeur dans un tableau trié en prenant, à chaque étape, le milieu de l'ensemble des valeurs possibles pour éliminer la moitié des possibilités.
On peut résumer le principe de fonctionnement de l'algorithme de recherche dichotomique par le schéma suivant :
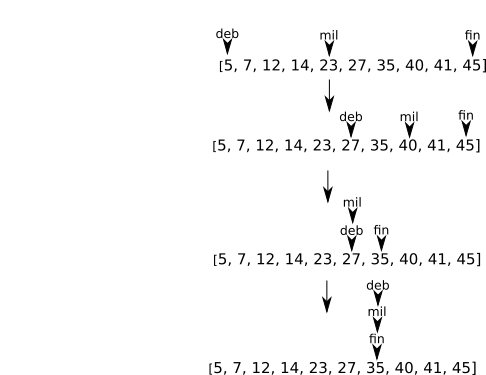
Il est aussi possible de représenter le principe de l'algorithme de recherche dichotomique avec le schéma suivant :

Faire tourner à la main
On rappelle l’algorithme de recherche dichotomique dans un tableau trié.
On dispose d’un tableau d’éléments triés par ordre croissant.
fonction appartient(tableau, element)
gauche = 0
droite = dernier indice
trouvé = faux
# AVANT
Tant que gauche <= droite et que trouvé = faux
milieu = (gauche + droite) // 2
# ICI
si tableau[milieu] = element alors trouvé = vrai
sinon si tableau[milieu] < element alors gauche = milieu + 1
sinon droite = milieu - 1
# LA
Retourner trouvé
a. Que retourne l’appel appartient ([1, 3, 5, 17, 17, 19], 3) ?
b. Compléter le tableau suivant pour l’appel précédent.
gauche |
milieu |
droite |
tableau[milieu] |
trouvé |
|
|---|---|---|---|---|---|
# AVANT |
0 | - | ? | - | ? |
# ICI |
0 | 2 | ? | ? | ? |
# LA |
0 | 2 | 1 | 5 | ? |
# ICI |
0 | 0 | 1 | 1 | ? |
# LA |
? | ? | ? | ? | ? |
# ICI |
? | ? | ? | ? | ? |
# LA |
? | ? | ? | ? | ? |
c. Dans l’exemple précédent, pourquoi sort-on de la boucle ?
On exécute l’appel appartient ([1, 3, 5, 17, 17, 19], 4) .
a. Que renvoie cet appel ?
b. Construire un tableau similaire au précédent.
c. Pourquoi sort-on de la boucle ?
d. Combien de fois passe-t-on par la ligne # ICI ?
On exécute l’appel appartient ([1, 13, 5, 17, 17], 13)
a. Quelle devrait-être la sortie de la fonction ? b. Qu’obtient-on en pratique ? On s’aidera d’un tableau similaire aux précédents. c. Expliquer le problème.
Programmer
Traduire en Python l’algorithme proposé dans l’exercice 3. On n’oubliera
pas les indications de type et la documentation.
En vous aidant de la fonction précédente, écrire le code de la fonction
suivante :
def dichotomie(tableau: list, element: int) ->int:
'''
cette fonction....
pré condition: ....
post condition:.....
'''
gauche = 0
droite =
while .......:
milieu = ....... // 2
if ............:
return True
elif.......:
gauche =..............
else:
droite = ................
return False
assert dichotomie([1,3,5,9,12,16,89],3)==True
assert dichotomie([1,3,5,9,12,16,89],52)==False
Complexité
Traduire en Python l’algorithme proposé dans l’exercice 3. On n’oubliera pas les indications de type et la documentation.
En vous aidant de la fonction précédente, écrire le code de la fonction suivante :
def dichotomie(tableau: list, element: int) ->int:
'''
cette fonction....
pré condition: ....
post condition:.....
'''
gauche = 0
droite =
while .......:
milieu = ....... // 2
if ............:
return True
elif.......:
gauche =..............
else:
droite = ................
return False
assert dichotomie([1,3,5,9,12,16,89],3)==True
assert dichotomie([1,3,5,9,12,16,89],52)==False
Nous avons vu précédemment que l'algorithme naïf de recherche d'un nombre dans une liste triée avait dans le pire des cas une complexité linéaire. Voyons si la dichotomie est plus avantageuse de ce point de vu.
Déterminez le nombre maximal de comparaisons nécessaires à la recherche d'un élément dans une liste, en complétant le tableau ci-dessous.
| Taille de la liste | 0 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | N |
| Recherche séquentielle | ||||||||||
| Recherche dichotomique |
Complexité
Pour étudier la complexité, nous allons nous intéresser à la boucle : au niveau de la boucle, combien doit-on effectuer d'itérations pour un tableau de taille n dans le cas le plus défavorable (l'entier x n'est pas dans le tableau t) ?
Sachant qu'à chaque itération de la boucle on divise le tableau en 2, cela revient donc à se demander combien de fois faut-il diviser le tableau en 2 pour obtenir, à la fin, un tableau comportant un seul entier ? Autrement dit, combien de fois faut-il diviser n par 2 pour obtenir 1 ?
Mathématiquement cela se traduit par l'équation $\frac{n}{2^a}=1$ avec a le nombre de fois qu'il faut diviser n par 2 pour obtenir 1. Il faut donc trouver a !
A ce stade il est nécessaire d'introduire une nouvelle notion mathématique : le "logarithme base 2" noté $log_2$. Par définition $log_2(2^x)=x$
Nous avons donc :
$\frac{n}{2^a}=1$ => $n=2^a$ => $log_2(n)=log_2(2^a)=a$, nous avons donc $a=log_2(n)$
Nous pouvons donc dire que la complexité en temps dans le pire des cas de l'algorithme de recherche dichotomique est $O(log_2(n))$
Afin de pouvoir comparer l'efficacité des différents algorithmes, voici une représentation graphique des fonctions $y=x$ (en rouge), $y=x^2$ (en bleu) et $y=log_2(x)$ (en vert)
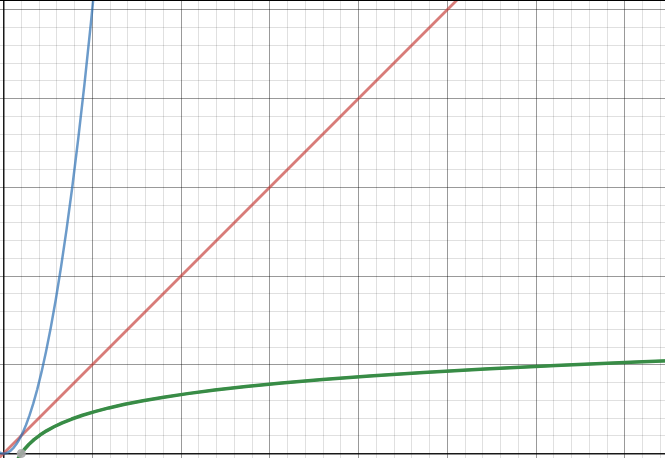
Comme vous pouvez le constater l'algorithme de recherche dichotomique est plus efficace que l'algorithme de recherche qui consiste à parcourir l'ensemble du tableau, car $x>log_2(x)$ quelque soit $x$. Cependant, il ne faut pas perdre de vu que dans le cas de la recherche dichotomique, il est nécessaire d'avoir un tableau trié, si au départ le tableau n'est pas trié, il faut rajouter la durée du tri.
Terminaison du programme
La fonction recherche_dichotomique contient une boucle non bornée, une boucle while, et pour être sûr de toujours obtenir un résultat, il faut s’assurer que le programme termine, que l’on ne reste pas bloqué infiniment dans la boucle.Pour prouver que c’est bien le cas, nous allons utiliser un variant de boucle.
Variant de boucle
Il s’agit d’une quantité entière qui :
Si l’on arrive trouver une telle quantité, il est évident que l’on a nécessairement sortir de la boucle au bout d’un nombre fini d’itérations,puisque un entier positif ne peut décroître infiniment
Preuve de la terminaison
Pour le cas qui nous occupe, un variant est très facile à trouver : il s’agit de la largeur de la quantité droite - gauche. La condition de boucle étant gauche <= droite, cela correspond exactement à ce que notre variant soit positif ou nul.
Montrons maintenant que le variant décroit strictement lors de l’exécution du corps de la boucle.
On commence par définir milieu = (gauche + droite) // 2
En particulier, on a alors gauche <= milieu <= droite.
Ensuite, trois cas sont possibles.
- si tableau[milieu] == val, on sort directement de la boucle à l’aide d’un return. La terminaison est assurée.
- si tableau[milieu] > val, on modifie la valeur de droite. En appelant droite2 cette nouvelle valeur, on a :
- droite2 - gauche < milieu - gauche <= droite - gauche
- sinon, on modifie gauche et on a de même :
- droite - gauche2 < droite - milieu <= droite - gauche
Ayant réussi à exhiber un variant pour notre boucle, nous avons prouvé qu’elle termine bien.
Sitographie
Voici une liste de sites traitant de la dichotomie :
Savoir faire et Savoir
- Écrire un algorithme de dichotomie.
- Montrer la terminaison de la recherche dichotomique à l’aide d’un variant de boucle.
- terminaison d'un algorithme
- variant de boucle