Nous allons étudier un algorithme d’apprentissage automatique (machine learning) dont l’objectif est de classifier des objets.
Entrainer une machine à apprendre n’est pas une idée récente, la première référence remontant à 1959 et est due à l’informaticien américain Arthur Samuel. Depuis le début des années 2000 ces méthodes rencontrent un important succès dû à la disponibilité de nombreux jeux de données et à l’amélioration de la performance des machines.
Principe
L’algorithme des k plus proches voisins est un algorithme d’apprentissage supervisé.
L’objectif de l’algorithme est de donner un label à des données.
On dispose de données labélisées qui servent à l’apprentissage et à la mesure de qualité des prédictions.
Une fois l’algorithme entrainé et testé on peut l’employer afin qu’il prédise le label d’une nouvelle donnée.

Classification
Le jeu de données doit :
- posséder une ou plusieurs caractéristiques,
- un label pour chaque donnée.
Dans l’exemple ci-dessous, les caractéristiques sont x_1 et x_2 et les labels sont A et B.
~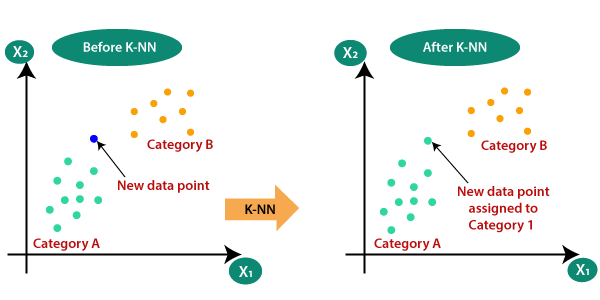
On ajoute un nouveau point (en bleu) dont on ne connait pas le label…
L’algorithme kNN va lui attribuer un label, en utilisant les données précédentes.
Le point se voit attribuer la catégorie A.
Algorithme kNN
- On choisit une valeur pour k,
- On calcule les distances d entre la nouvelle donnée N et ses voisins X_i déjà classifiés.
- Parmi les points X_i, les k plus proches de N sont retenus.
- On attribue à N le label majoritaire parmi les k plus proches voisins.
Choix d’une valeur de k
On peut choisir la valeur que l’on veut mais …
- Une valeur impaire produit des ex-aequos,
- Une valeur trop faible va rendre le résultat sensible au bruit,
- Une valeur trop grande risque de faire sortir des classes.
Par bruit on entend bruit statistique, les faibles variations de mesure ou de qualité dans les données.
Apprentissage
Contrairement à de nombreux algorithmes plus complexes, la phase d’apprentissage est immédiate. Il suffit de découper notre jeu de données initiales (labélisées) en deux lots. Le premier servira à apprendre le second à tester.
La phase de test permet de mesurer la qualité des prédictions contre des données pour lesquelles on connait déjà la classe.
Exemple
On considère deux espèces, les orques et les chevaliers.
On a des raisons de supposer qu’on peut les distinguer en mesurant leur courage et leur force .
| courage | force | classe |
|---|---|---|
| 0.17 | 2.84 | chevalier |
| 0.24 | 3.82 | chevalier |
| 0.24 | 3.39 | chevalier |
| 0.2 | 2.60 | chevalier |
| 0.25 | 4.21 | orque |
| 0.47 | 4.64 | orque |
| 0.47 | 4.48 | orque |
| 0.49 | 4.9 | orque |
| 0.46 | 4.08 | orque |
On ajoute un nouvel élément dont on connait les caractéristiques mais pas la catégorie :
Nouveau : courage = 0.19, force = 2.91
À quelle espèce appartient-il ?
On complète les données précédentes avec la distance séparant cet élément des précédents.
On emploie ici une distance Euclidienne usuelle : AB = \sqrt{ (x_B - x_A)^2 + (y_B - y_A)^2 }
| distance | classe |
|---|---|
| 0.072 | chevalier |
| 0.911 | chevalier |
| 0.482 | chevalier |
| 0.310 | chevalier |
| 1.301 | orque |
| 1.752 | orque |
| 1.594 | orque |
| 2.012 | orque |
| 1.200 | orque |
Choisissons k=3, on ne conserve que les trois éléments les plus proches de notre nouvel élément :
| distance | classe |
|---|---|
| 0.072 | chevalier |
| 0.310 | chevalier |
| 0.482 | chevalier |
La classe majoritaire est
chevalier, et c’est celle qu’on attribue à notre nouvel élément.
Complexité
Intéressons-nous à la complexité de cet algorithme. Le résultat sera décevant !
-
Afin de calculer les distances, un parcourt du tableau suffit : O(n)
-
Mais… on décide de converver les k plus proches… on pourrait être tenté de trier et la complexité deviendrait O(n\log(n)) ou pire, O(n^2) si on utilise un des tris étudiés cette année…
C’est une mauvaise idée, on peut parfaitement déterminer les plus proches en un seul parcours. À chaque fois qu’on rencontre une donnée plus proche, on l’insère dans la liste à sa place.
Ainsi la complexité devient O(k \times n), mais k étant constant : O(n).
L’algorithme de k plus proches voisins, bien implanté, est linéaire en la taille des données.
Choix d’une distance et pré-traitement des données
Il existe de nombreuses manières de calculer la distance entre des objets, la distance usuelle, vue en seconde n’en est qu’une parmi d’autre.
Selon le type de donnée, on peut amené à changer la distance employée.
C’est en particulier le cas lorsqu’on utilise avec des données qualitatives (couleur des yeux, plat favori etc.).
Par ailleurs, ainsi qu’on peut le remarquer dans l’exemple précédent, les données ne sont pas toutes du même ordre de grandeur. Cela engendre un problème : les données les plus grandes vont peser plus lourdement dans le calcul de distance.
Afin de pallier cette difficulté on normalise les données, c’est à dire qu’on divise toutes les données d’une même catégorie par leur valeur maximale afin de les ramener entre 0 et 1.
Lourdeur de l’algorithme
Bien qu’il soit linéaire, l’algorithme kNN présente un défaut majeur :
À chaque nouvelle donnée, il faut parcourir tout le tableau pour la classifier. Plus on ajoute de données, plus il est lent.
Utilisations dans l’industrie
Des adaptations de kNN sont employées en permanence. L’exemple auquel vous avez tous déjà été confronté est celui de la recommandation après consultation d’un contenu.
Vous regardez une vidéo en streaming et on vous propose d’autres vidéos similaires, susceptibles de vous intéresser. Comment faire ?
On attribue à chaque vidéo des caractéristiques et on lui donne un label en déterminant les autres vidéos dont elle est le plus proche.
On utilise plusieurs labels différents (“intérêt chez les moins de 18”, “nombre de scènes d’action” etc.) et on détermine les plus représentatifs.
Bien sûr, d’autres traitements sont effectués afin d’accélérer le procédé sans perdre trop de précision sur les recommandations.