Les arbres
COURS
Nous allons travailler sur la structure de donnée "arbre". Cette structure n'est pas linéaire mais hiérarchique.
Arbre
Un arbre est une structure de donnée constituée de nœuds.
Le sommet de l'arbre s'appelle la racine.
Le nœud B situé sous un nœud A est appelé enfant du nœud A
Un nœud qui ne possède pas d'enfant est appelé feuille.
Les nœuds autre que la racine et les feuilles sont appelés nœuds internes.
Une branche est une suite de nœud consécutifs de la racine vers une feuille.
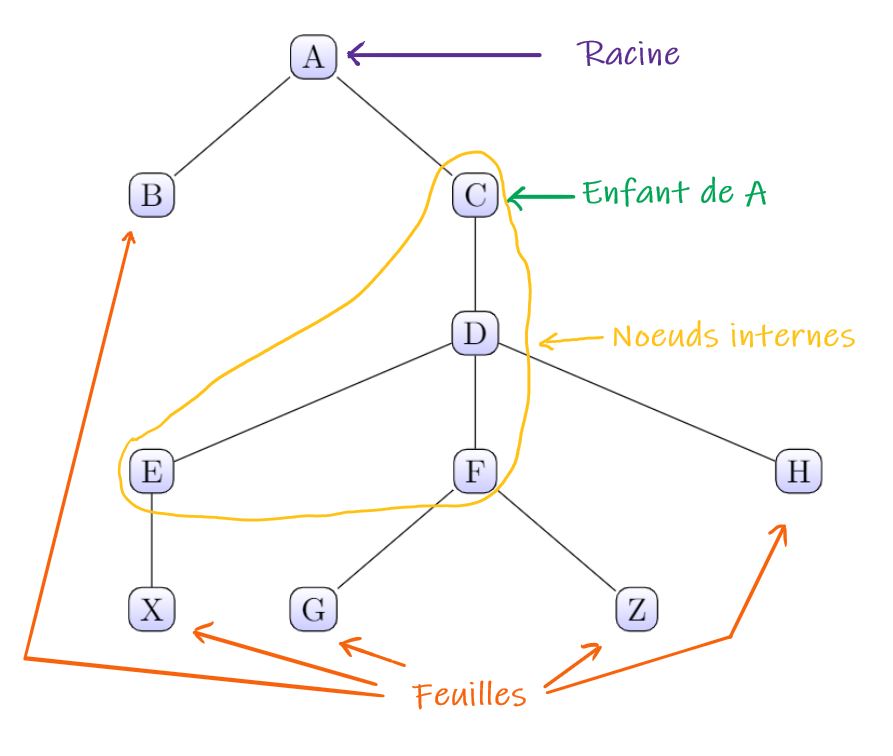
Dans cet arbre:
- il y a 10 nœuds.
- Le nœud A est la racine
- Il y a 5 feuilles donc 5 branches.
- Le nœud D est l'enfant du nœud C.
- Il y a 4 nœuds internes.
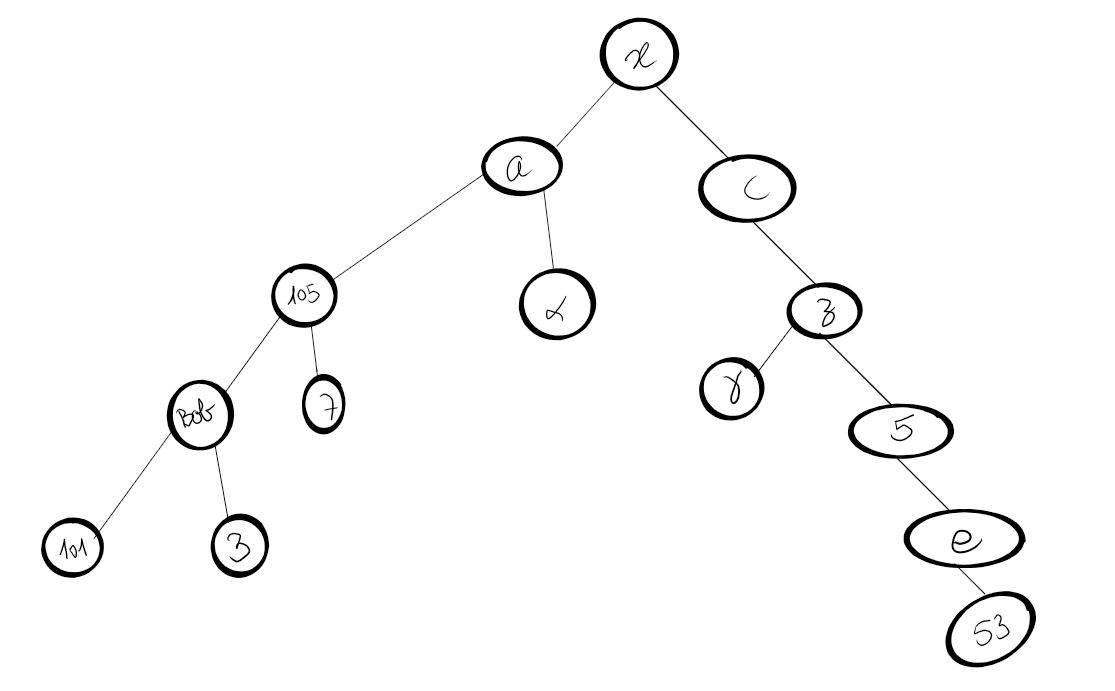
On donne l'arbre suivant :
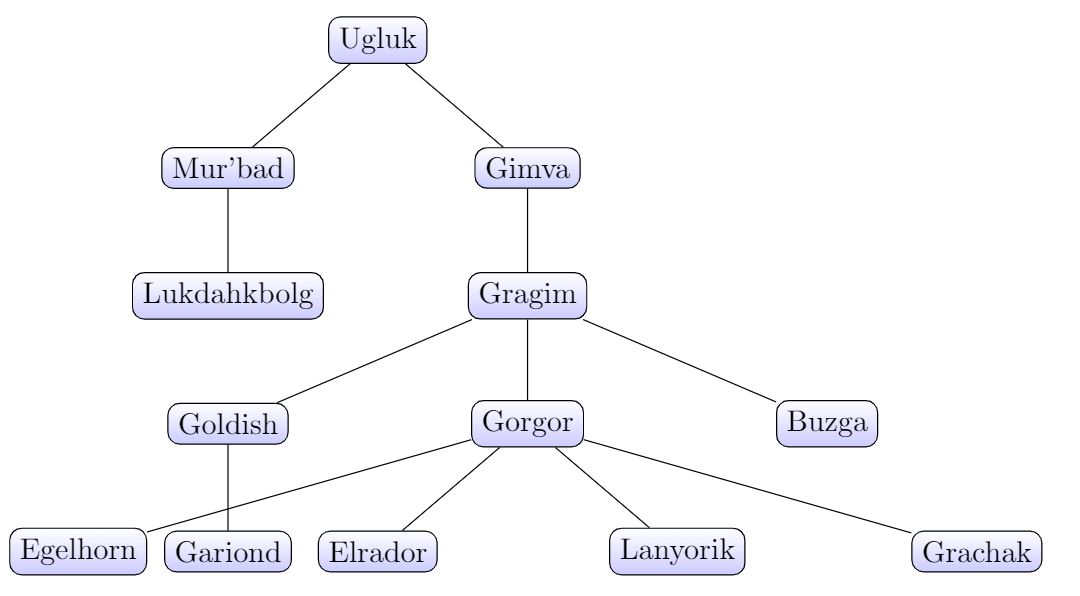
- Quelle est la racine de cet arbre?
- Combien ya-t-il de nœuds?
- Combien ya-t-il de feuilles?
- Combien ya-t-il de branches?
- L'ensemble des nœuds internes compte combien d'éléments?
- Quels sont les enfants de Gragim?
On peut caractériser un arbre par différentes caractéristiques :
- Son arité : le nombre maximal d'enfant qu'un nœud peut avoir.
- Sa taille : le nombre de nœud qui le compose.
- Sa hauteur : le nombre de nœud que constitue la branche contenant le plus de nœuds sans compter la racine.
On reprend l'arbre de la définition d'un arbre :

- L'arité de cet arbre est 3.
- La taille de cet arbre est 10.
- La hauteur de cet arbre est 4.
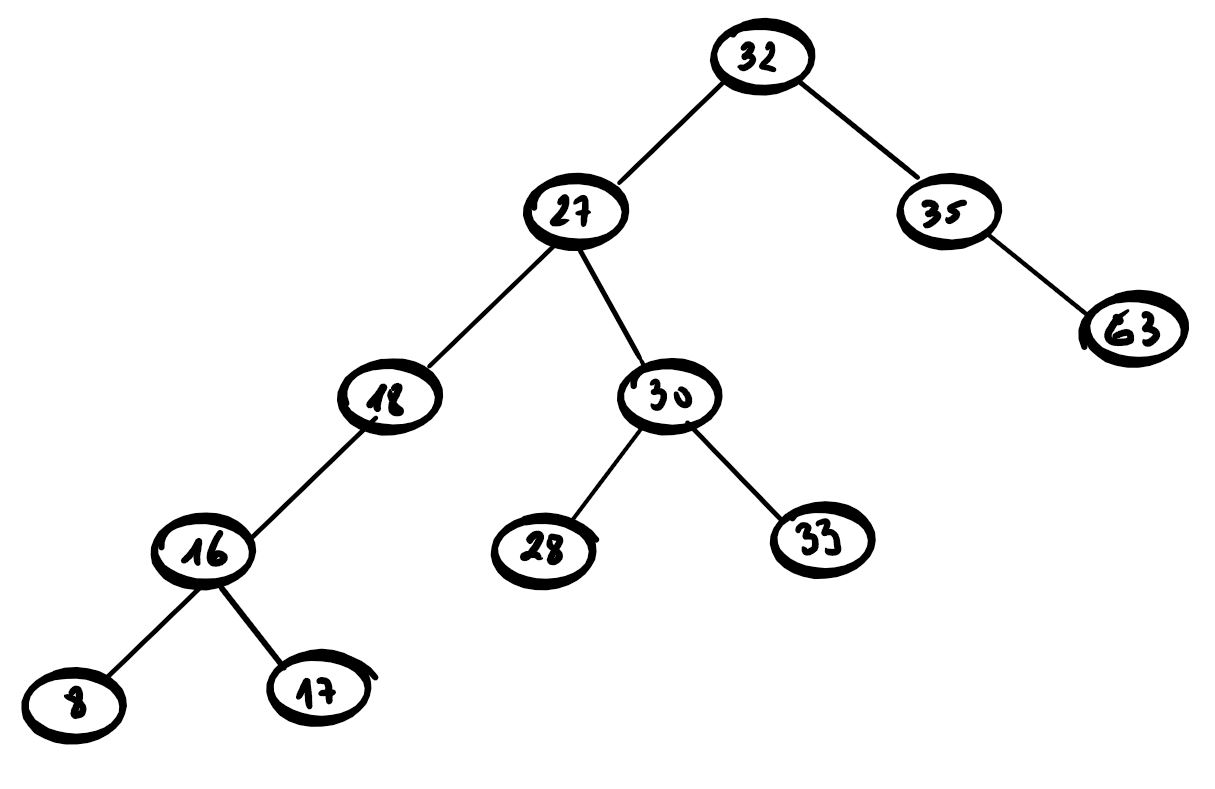
On donne l'arbre suivant :
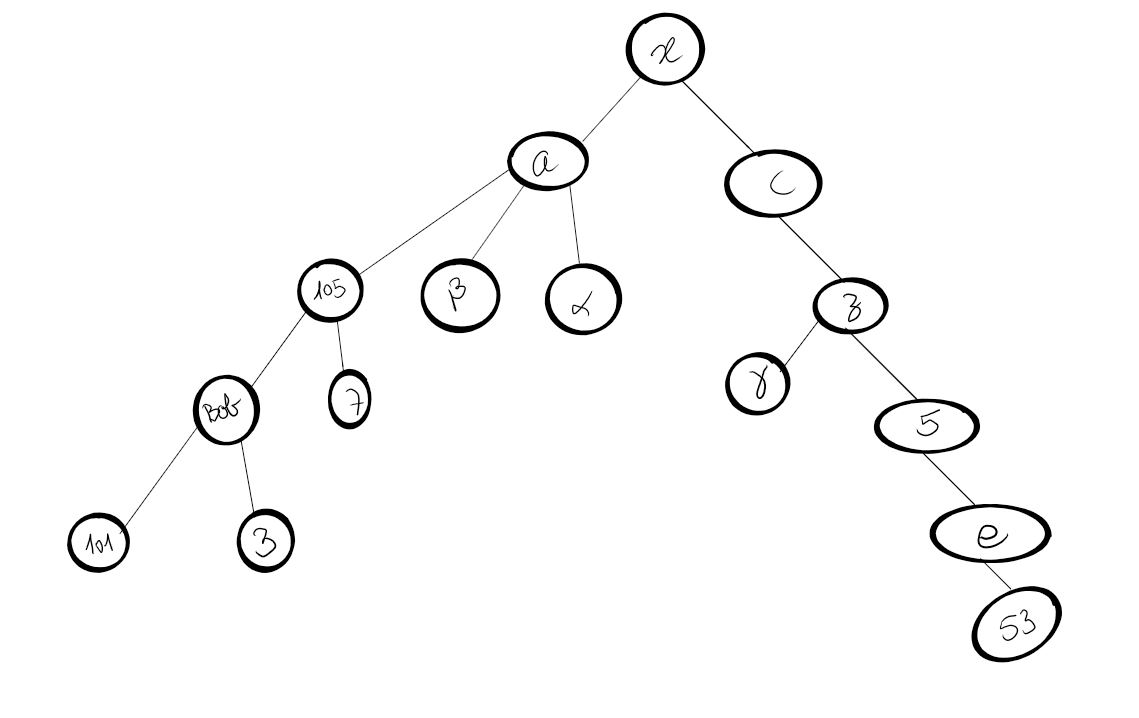
Déterminer l'arité, la taille et la hauteur de cet arbre.
Prenons l'exemple de notre réseaux, imaginons que winapps soit la racine.
Représenter une partie:-) de l'arborescence des répertoires et des fichiers à l'aide d'un arbre.
Arbres binaires
Définitions
Arbres binaires
On appelle arbre binaire un arbre d'arité 2.
Les arbres binaires sont constitués de nœuds de 0, 1 ou 2 enfants.
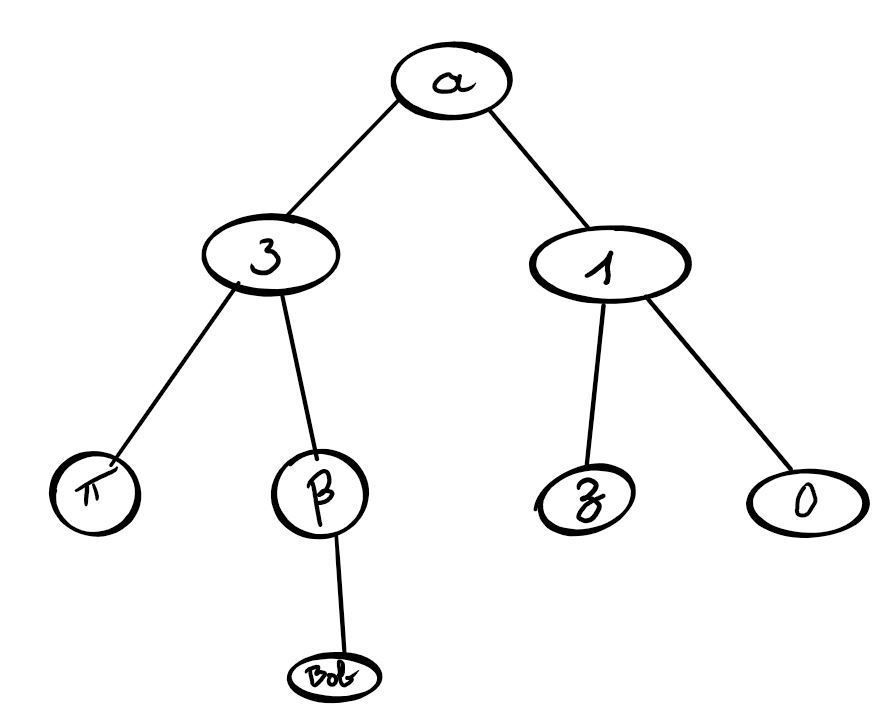
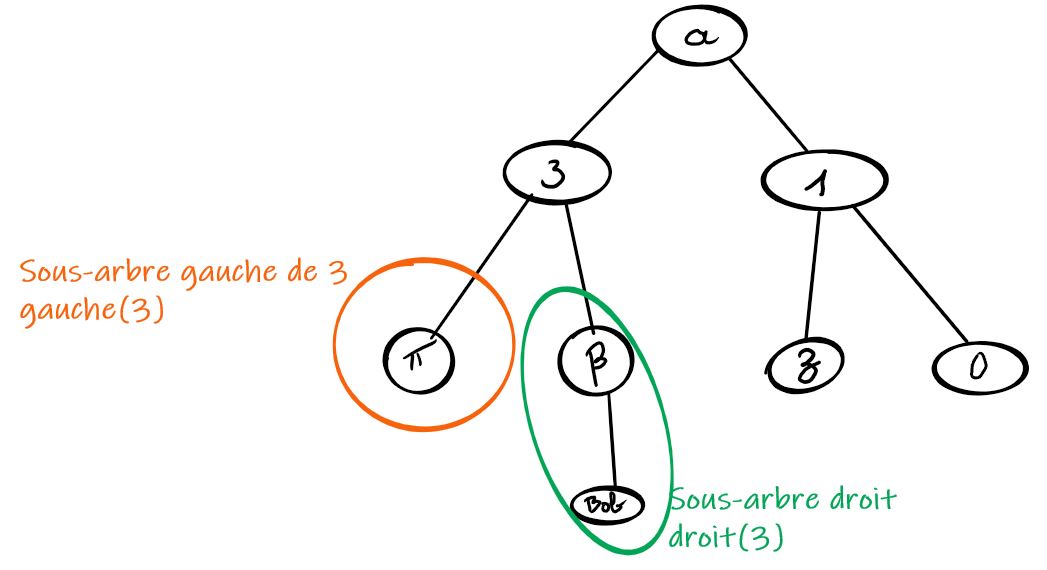
Sous-arbre droit/gauche
Quand un nœud a deux enfants, il possède un sous-arbre gauche et un sous-arbre droit.
Pour un nœud \alpha, on notera :
- gauche(\alpha) le sous-arbre gauche du nœud \alpha;
- droit(\alpha) le sous-arbre droit du nœud \alpha.
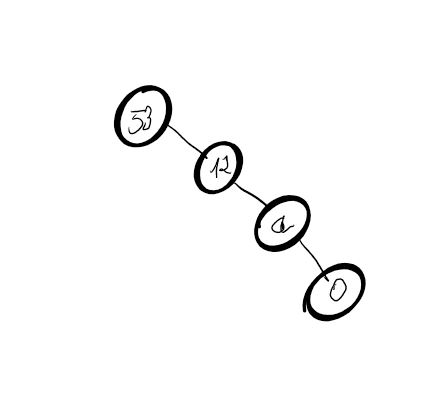
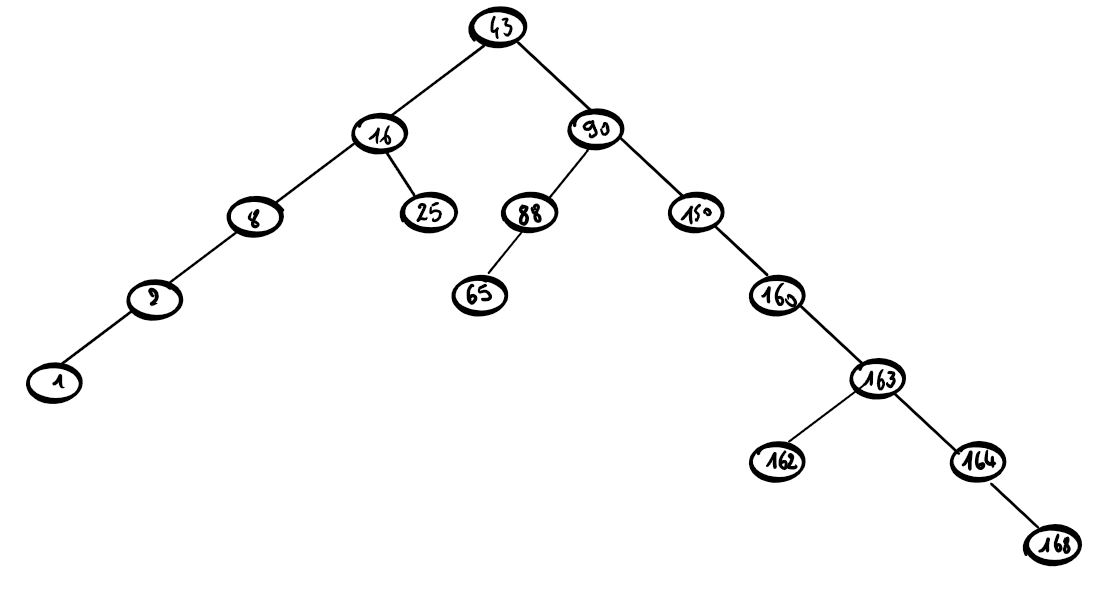
Parmi les arbres suivants lesquels sont binaires?
Mesures sur les arbres binaires
Les arbres binaires étant particuliers, on peut calculer un certains nombres de caractéristiques d'un arbre binaire.
La taille d'un arbre B correspond au nombre de ses nœuds, elle est définie par :
- Taille(B)=0, si B est un arbre vide
- Taille(B)=1+Taille(gauche(B))+Taille(droit(B))
On donne l'arbre suivant :
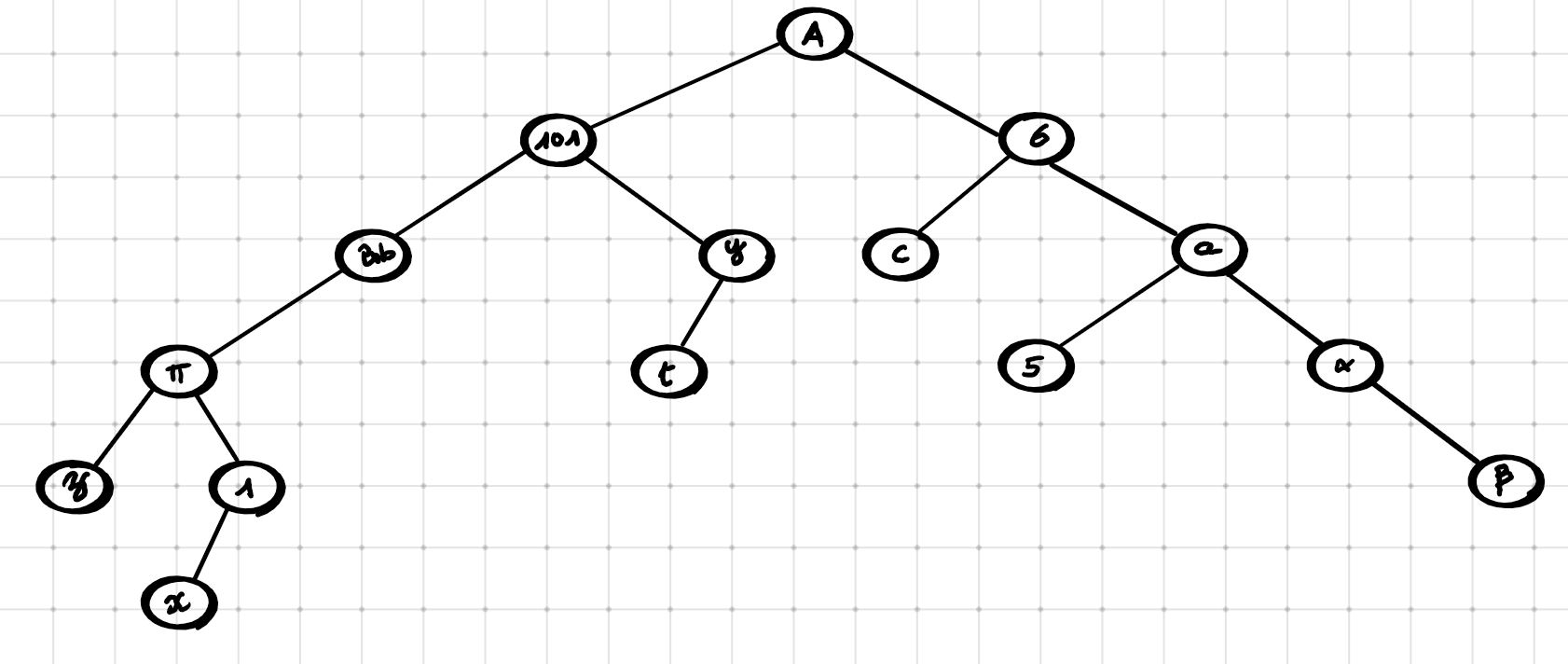
Déterminer la taille de cet arbre.
La hauteur d'un nœud ou la profondeur de x correspond au nombre d'arêtes au dessus x pour revenir à la racine, elle est définie par :
- HauteurDeNoeud(x)=0, si x est la racine de l'arbre.
- HauteurDeNoeud(x)=1+HauteurDeNoeud(y) si y est le père de x.
On donne l'arbre suivant :

Déterminer la hauteur des nœuds Bob.
La hauteur d'un arbre B correspond au nombre d'arêtes entre a racine et la feuille la plus éloignée :
- Hauteur(B)=Max(HauteurDeNoeud(x)), où x qui décrit l'ensemble des nœuds de B.
On donne l'arbre suivant :

Déterminer la hauteur de cet arbre.
La longueur de cheminement d'un arbre B correspond à la somme des hauteurs de chacun des noeuds. :
- LC(B)=somme de tous les H(x), où x qui décrit l'ensemble des nœuds de B.
On donne l'arbre suivant :

Déterminer la longueur de cheminement de cet arbre.
La longueur de cheminement externe d'un arbre B correspond à la somme des hauteurs de chacune des feuilles :
- LCE(B)=somme de tous les H(f), où f décrit l'ensemble des feuilles de B.
On donne l'arbre suivant :

Déterminer la longueur de cheminement externe de cet arbre.
La longueur de cheminement interne d'un arbre B correspond à la somme des hauteurs des nœuds internes de B :
- LCI(B)=somme de tous les H(x), où x décrit l'ensemble des nœuds internes de B.
On donne l'arbre suivant :

Déterminer la longueur de cheminement interne de cet arbre.
Déterminer une relation entre LC(B), LCE(B) et LCI(B).
La profondeur moyenne d'un arbre B est définie par :
PM(B)=LC(B)/T(B)
On donne l'arbre suivant :

Déterminer la profondeur moyenne de cet arbre.
La profondeur moyenne externe d'un arbre B est définie par :
PME(B)=LCE(B)/NF
On donne l'arbre suivant :

Déterminer la profondeur moyenne externe de cet arbre.
La profondeur moyenne interne d'un arbre B est définie par :
PMI(B)=LCI(B)/(T(B)-NF)
On donne l'arbre suivant :

Déterminer la profondeur moyenne interne de cet arbre.
La longueur de cheminement et la profondeur moyenne seront utiles pour les algorithmes sur les arbres binaires.
On donne l'arbre B suivant :
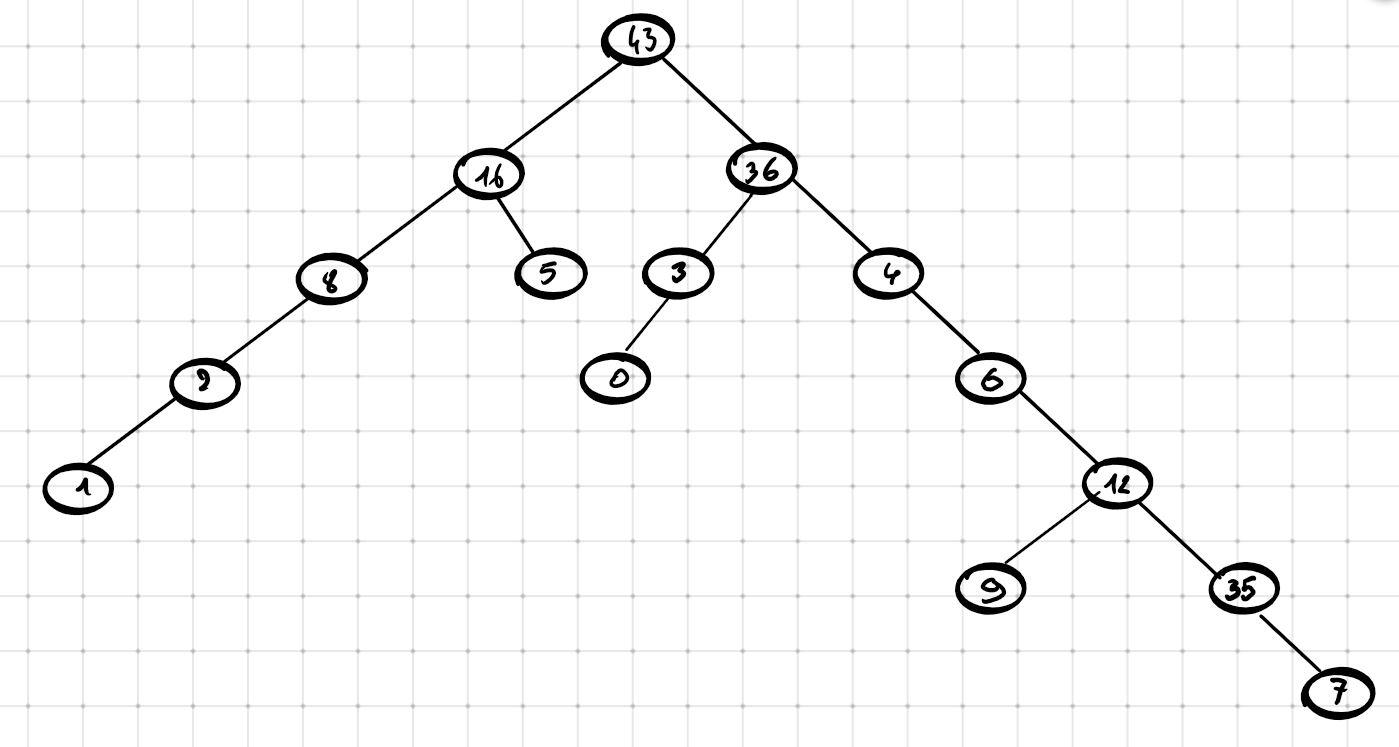
Déterminer :
- la racine
- le nombre de feuilles
- le nombre de branches
- l'arité
- sa taille T(B)
- La hauteur de B, H(B)
- LC(B)
- LCE(B)
- LCI(B)
- PM(B)
- PME(B)
- PMI(B)
Arbre binaire de recherche
Un arbre binaire de recherche est un arbre binaire dans lequel l'étiquette d'un nœud est appelé clé et est un entier. L'arbre binaire vérifie deux propriétés :
- Les clés de tous les nœuds du sous-arbre gauche d'un nœud x sont inférieures ou égales à la clé de x.
- Les clés de tous les nœuds du sous-arbre droit d'un nœud x sont strictement supérieures à la clé de x.
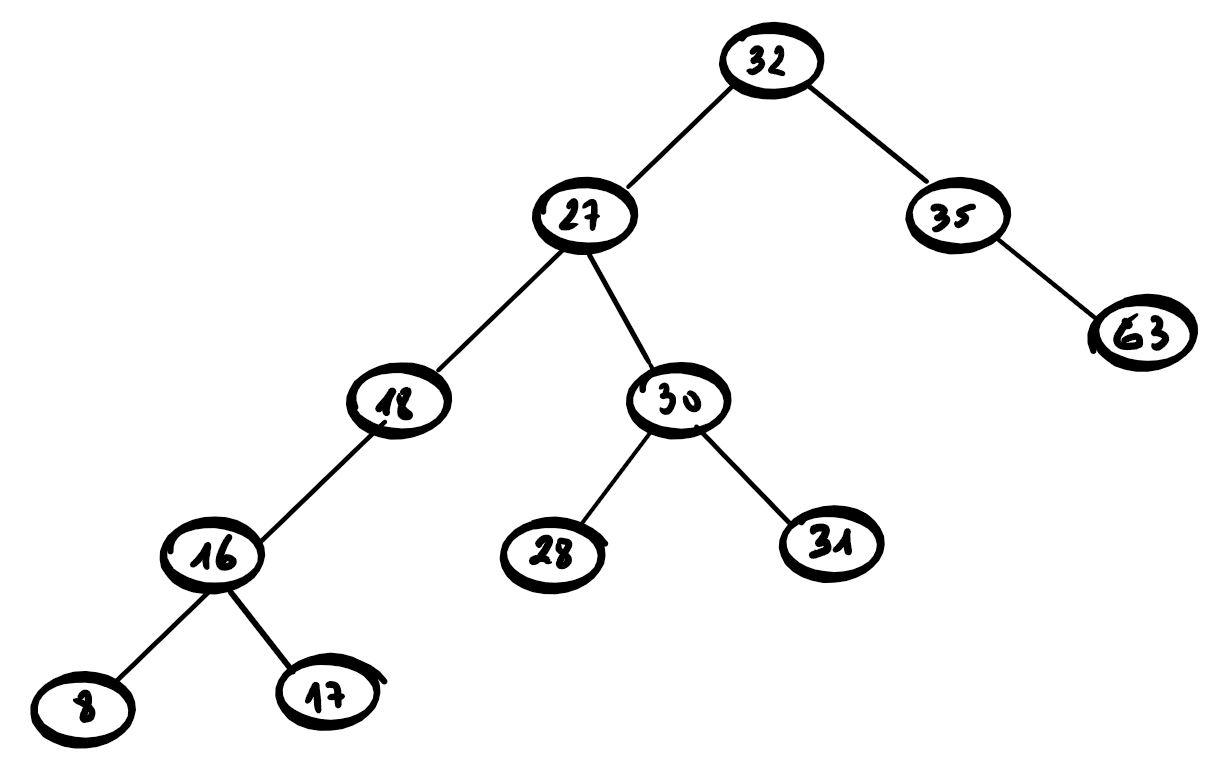
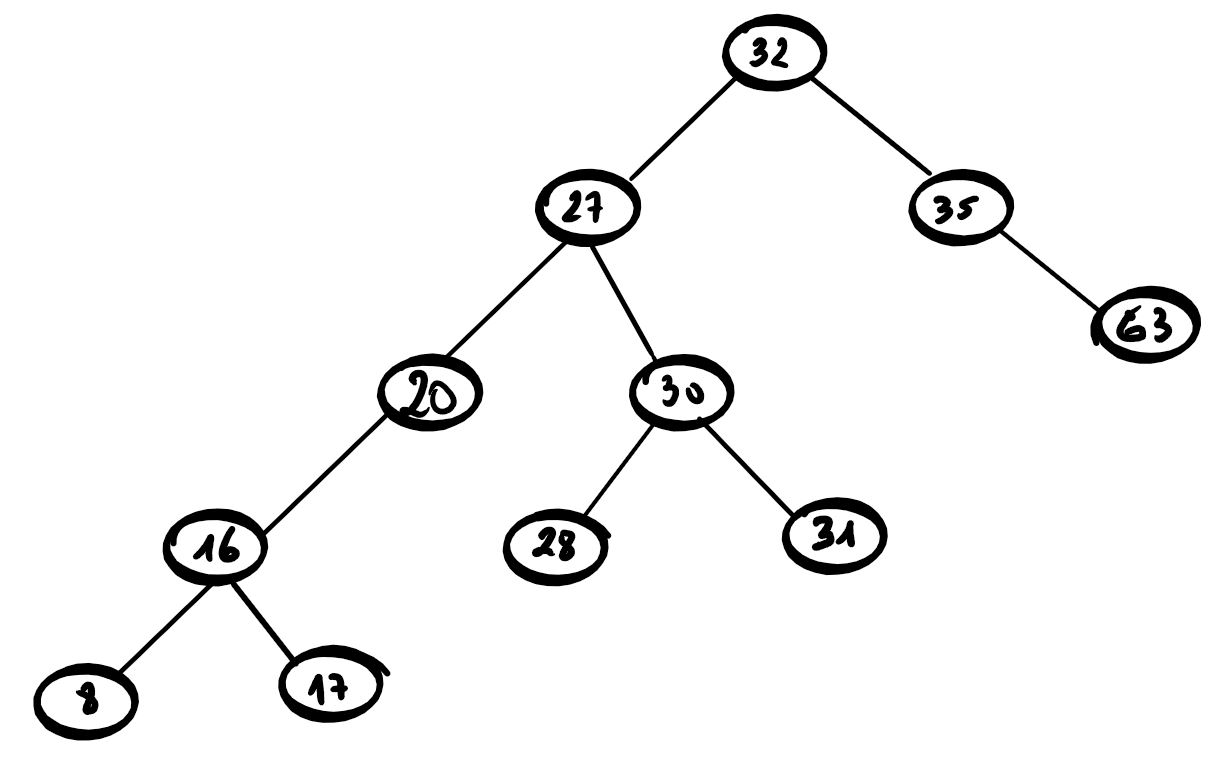
Quels sont parmi les arbres proposés ci-dessous les arbres binaires de recherche?
Compléter cet arbre pour que ce soit un arbre binaire de recherche :

Un étiquetage intéressant d'un arbre de recherche est le suivant :
- La racine est étiquetée 1
- La premier nœud du sous arbre gauche prend l'étiquette de son père auquel on ajoute un 0
- La premier nœud du sous arbre droit prend l'étiquette de son père auquel on ajoute un 1
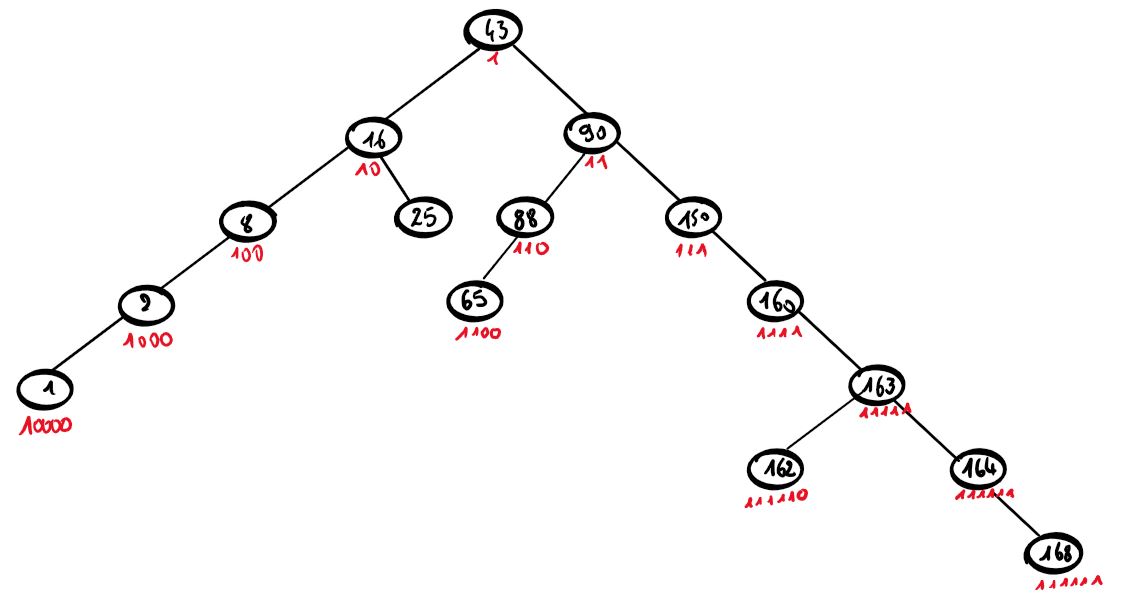
Etiqueter comme l'exemple précédent l'arbre suivant :

On observe que les étiquettes des nœuds de profondeur p sont constituées de p + 1 bits, et sont deux à deux distinctes. On en déduit que toutes les étiquettes des nœuds d’un même arbre sont deux à deux distinctes.
Les étiquettes peuvent être vues comme les écritures de numéros en base 2 : on a ainsi numéroté les différents nœuds de l’arbre.