Un peu de théorie

On dit également qu'un problème est décidable s'il existe un algorithme capable de résoudre le problème en un nombre fini d'étapes.

Pendant très longtemps les mathématiciens ont considérés (intuitivement) que tout problème avait une solution, et qu'il suffisait de trouver la méthode qui permettrait de résoudre le problème.

Puis la question s'est naturellement posée notamment lors de la publication des 23 problèmes (1900) de David Hilbert.

Certains d'entre eux ne sont toujours pas résolus comme la conjecture de Goldbach qui affirme que tout nombre entier pair supérieur à 3 peut s'écrire comme la somme de deux nombres premiers (12 = 5 + 7).

Depuis les travaux de Kurt Gödel (1931) et d' Alan Turing (1936), on sait maintenant qu'il existe une infinité de problèmes non décidables (de fonctions non calculables).

Ces travaux ont conduit à déterminer les contours de ce qui est faisable ce qui a permis à l'informatique de naître.

La machine de Turing

introduction

Essayons de faire quelque chose de paradoxal : montrer concrètement comment marche une machine abstraite !

Car c’est bien une machine abstraite qu’Alan Turing a inventée pour expliquer la notion de « procédure mécanique » : on parle d’algorithme. Cette machine est la plus élémentaire possible destinée à mettre en œuvre ces mécanismes de calcul, numériques ou symboliques, comme le font notamment les ordinateurs. Ne perdons pas de vue que lorsqu’Alan Turing décrit sa machine dans un article en 1936, les ordinateurs n’existent pas encore !

Comment ça fonctionne?

La machine imaginée par Turing comporte un ruban divisé en cases, dans lesquelles elle peut écrire des symboles. La machine ne peut lire qu’une seule case à la fois, de même elle écrit dans une seule case et décale le ruban d’une seule case vers la gauche ou vers la droite. Les symboles sont en nombre fini. Pour que sa machine fonctionne comme une machine à calculer en binaire, Turing envisage le cas particulier où les symboles utilisés sont 0 et 1.

L’entrée du programme est une liste de symboles binaires, écrits sur le ruban, matérialisé par les cases successives (en bas de l’animation). Une fois le calcul effectué, c’est sur ce ruban que sera écrit le résultat du calcul, la sortie du programme. À chaque instant, le ruban mémorise l’état du calcul. Voilà la forme la plus simple de mémoire mécanique !

À chaque programme correspond une description sous forme de table (à droite de l’animation). Chacune des lignes de cette table est associée à un état et spécifie les actions à effectuer quand la machine est dans cet état, en fonction du symbole présent sous la tête de lecture. Ces actions peuvent être l’écriture d’un symbole (ici un 0 ou un 1) et le déplacement du ruban d’une case à droite ou à gauche. La ligne spécifie également le nouvel état après l’exécution des actions. La machine s’arrête quand un état marqué comme final est atteint.

Turing a également prévu que les programmes, tels qu’ils sont décrits par la table, puissent eux aussi être codés en binaire et inscrits sur un deuxième ruban. Chaque code correspond alors à une instruction possible. Le calcul se déroule automatiquement en passant d’une instruction à une autre. Comme il est possible d’inscrire sur ce deuxième ruban toutes sortes de programmes et de les exécuter, ce mécanisme va pouvoir faire (avec beaucoup de patience !) tout ce qu’un ordinateur peut faire. On parle de machine de Turing universelle.

petit exemple avec l'incrémentation binaire (+1)

Pour ajouter 1 à un nombre binaire, on utilise la table d’addition suivante :

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10 : on pose 0, et on retient 1

Si le nombre binaire en entrée se termine par 0, par exemple :

1001010 + 1 = 1001011

dans ce cas, il suffit de remplacer le dernier 0 par un 1. On parcourt le nombre de gauche à droite, et lorsqu’on arrive à la fin, si on trouve un 0, on le remplace par un 1 et on passe à l’état final.

Si le nombre binaire en entrée se termine par 1, par exemple :

1001011 + 1 = 1001100

dans ce cas, après avoir parcouru le nombre de gauche à droite, on revient de droite à gauche, tant qu’on trouve un 1, on le remplace par un 0, lorsqu’on trouve la première occurrence de 0, on la remplace par 1 puis on passe à l’état final.

Cas particulier de nombre se terminant par 1, un nombre peut être formé seulement par des 1, par exemple :

1111111 + 1 = 10000000

dans ce cas, on remplace tous les 1 par 0 et on insère un 1 dans la première case vide à gauche.

Passons maintenant à la programmation de notre machine.

La table d’actions utilisée est la suivante :

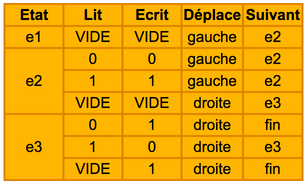
Pour mieux comprendre: à l'aide d'une feuille de brouillon représentant le ruban, réaliser les étapes du tableau ci-dessus.

Pour aller plus loin: Les théorèmes d'incomplétude de Gödel