Introduction

Les objets du numérique, qu’ils soient matériels (ordinateurs, smartphones, objets connectés, réseaux informatiques) ou immatériels (logiciels, données, systèmes d’information), sont de plus en plus souvent la cible d'attaques. Le domaine de la cybersécurité développe des méthodes en amont pour éviter ou détecter de tels actes malveillants.

Les défis qu’il soulève représentent un enjeu majeur aussi bien au niveau scientifique et technologique qu’au niveau sociétal, économique, politique et militaire.

Des méthodes de chiffrement sont utilisées depuis l’antiquité, et l’une des utilisations les plus célèbres pour cette époque est le chiffre de César, nommé en référence à Jules César qui l’utilisait pour ses communications secrètes. Il s'agit d'un chiffrement par décalage : l'idée est de définir une clé de chiffrement, qui est un entier compris entre 1 et 26 correspondant au décalage à effectuer dans l'alphabet pour remplacer chaque lettre. Par exemple, avec un décalage de 3 vers la droite, A est remplacée par D, B par E, ..., Z par C :

Illustration du chiffre de César
Crédit : Cepheus, Domaine public, via Wikimedia Commons

La méthode du chiffre de César n’est pas infaillible ! En effet, il n’y a au pire que 26 clés à tester pour décrypter un message codé, il suffit de toutes les tester. Et mieux : il peut très facilement être « cassé » par analyse de fréquences. Par exemple, pour un message écrit en français, il y a de fortes chances que la lettre qui apparaît le plus souvent corresponde à la lettre E...

Les méthodes de chiffrement actuelles sont bien plus sophistiquées que le chiffre de César, néanmoins elles sont toujours basées sur une (ou plusieurs) clé(s) de chiffrement, mais elles assurent qu’une personne qui ne possède pas la clé ne puisse pas comprendre le message.

Vous utilisez le chiffrement tous les jours des dizaines de fois, sans forcément le savoir : c'est le cas lorsque vous envoyez un message ou appelez quelqu'un via une application, lorsque vous postez quelque chose sur un réseau social, lorsque vous consultez un site Web, lorsque vous payez en ligne, lorsque vous vous connectez à un réseau Wi-Fi sécurisé, etc.

Il existe deux grandes catégories de chiffrement : les chiffrements symétriques et les chiffrements asymétriques. Nous allons décrire les principes de ces deux types de chiffrement puis nous terminerons en expliquant le fonctionnement du protocole HTTPS utilisé sur le Web pour sécuriser toutes nos communications.

Chiffrement symétrique

Un chiffrement symétrique, également dit à clé secrète est la plus ancienne forme de chiffrement : elle est basée sur une clé qui permet à la fois de chiffrer et de déchiffrer un message (le chiffre de César, par exemple, est symétrique).

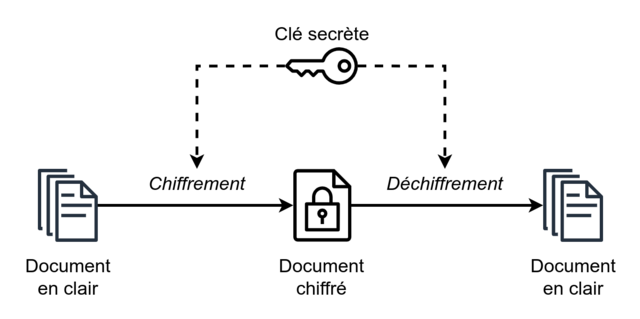
Schéma du chiffrement symétrique.
Crédit : MarcT0K (icônes par JGraph), CC BY-SA 4.0, via Wikimedia Commons

La clé doit absolument rester secrète car sa connaissance permet de déchiffrer le message. Il faut donc que la clé soit suffisamment compliquée pour ne pas être attaquée par force brute (on a vu qu'avec le code de César, il n'y a que 25 clés possibles).

Une attaque par force brute consiste à énumérer toutes les clés possibles jusqu'à trouver la bonne. Il faut donc qu'il y en ait beaucoup trop à tester afin de garantir une certaine sécurité.

Chiffrement XOR

Un algorithme de chiffrement symétrique plus évolué est le chiffrement XOR basé sur l'opérateur logique XOR, dont le nom vient de l'anglais eXclusive OR (on dit OU exclusif en français). Cet opérateur se note souvent $\oplus$ et sa table de vérité est la suivante :

$x$	$y$	$x \oplus y$
0	0	0
0	1	1
1	0	1
1	1	0

Pour chiffrer un message il suffit de choisir une clé de chiffrement, que l'on répète autant que nécessaire pour obtenir une clé de la même longueur que le messsage à chiffrer, et d'appliquer l'opération XOR bit à bit entre le message et la clé.

Pour chiffrer le message "MOUNIER" avec la clé "info", on obtient :

Message	M	O	U	N	I	E	R
Clé (répétée si nécessaire)	i	n	f	o	i	n	f
Message (en binaire)	01001101	01001111	01010101	01001110	01001001	01000101	01010010
Clé (en binaire)	01101001	01101110	01100110	01101111	01101001	01101110	01100110
Message chiffré (en binaire) obtenu par XOR	00100100	00100001	00110011	00100001	00100000	00101011	00110100
Message chiffré (en hexadécimal)	24	21	33	21	20	2B	34
Message chiffré (en ASCII)	$	!	3	!	(espace)	+	4

Il est très facile de déchiffrer un message : il suffit d'appliquer à nouveau l'opération XOR entre le message chiffré et la clé pour retrouver le message de départ car l'opération XOR vérifie la propriété suivante : $(x \oplus y) \oplus y = x$ (essayez !)

La méthode de chiffrement XOR décrite au-dessus n'est en réalité pas sécurisée si on utilise toujours la même clé et que nous la répétons pour atteindre la taille du message à coder. Mais en adaptant légèrement l'idée, on peut parvenir à un chiffrement théoriquement incassable. Cette amélioration, qui porte le nom de masque jetable ou de chiffre de Vernam, est la suivante :

• la clé doit être une suite de caractères aussi longue que le message à chiffrer
• les caractères composant la clé doivent être choisis de façon totalement aléatoire
• chaque clé ne doit être utilisée qu'une seule fois

Mais le fait de devoir générer aléatoirement une nouvelle clé à chaque chiffrement rend le chiffre de Vernam inutilisable en pratique. Mais il existe des méthodes de chiffrement tout aussi robustes qui permettent de conserver la même clé pour une série d'échanges, comme le chiffrement AES.

Chiffrement AES (Advanced Encryption Standard)

Le chiffrement symétrique le plus utilisé actuellement est le chiffrement AES (pour Advanced Encryption Standard, soit « norme de chiffrement avancé »). Il est très similaire au chiffrement XOR ou au masque jetable :

• une clé complètement aléatoire de taille 128, 192 ou 256 bits est créée
• cette clé est utilisée pour transformer le message à chiffrer mais avec davantage d'opérations qu'un simple XOR

Il n'existe aucune attaque connue efficace à ce jour pour casser le chiffrement AES (c'est-à-dire pour trouver la clé avec une méthode efficace). Le seul moyen de trouver la clé est de tester toutes les clés possibles, on appelle cela une attaque par force brute. Avec une clé de 256 bits (pour le chiffrement AES-256), il y a $2^{256}$ clés possibles, ce qui fait environ $1.16\times 10^{77}$ clés à tester. L'âge de l'univers étant de $10^{10}$ années, et en supposant que l'on puisse tester 1 000 milliards de clés par seconde (soit $3,2\times 10^{19}$ clés par an), il faudra encore attendre plus d'un milliard de milliards de milliards de milliards de fois l'âge de l'univers pour tester toutes les clés possibles 🤯🤯🤯

Le chiffrement AES (avec des clés de taille 192 et 256) est utilisé par exemple par la NSA pour tous ses documents classés secret défense. Il est aussi utilisé par les gestionnaires de mots de passe, pour chiffrer des bases de données, etc.

Chiffrement asymétrique

Le chiffrement asymétrique, aussi appelé chiffrement à clé publique, permet d'assurer des communications confidentielles sans que cela repose sur une clé secrète partagée au préalable comme c'était le cas pour le chiffrement symétrique.

Les algorithmes de cryptographie asymétrique sont basés sur l'utilisation d'une clé publique, c'est-à-dire connue de toutes et tous. Cette clé publique, associée à une clé privée, est utilisée dans des protocoles qui permettent de sécuriser les communications.

Échange de clés de Diffie-Hellmann

C'est en 1976 que Whitfield Diffie et Martin Hellmann ont présenté un protocole permettant à deux participants (appelés par convention Alice et Bob) de construire une clé secrète partagée de manière sûre, à partir d'une clé publique connue de tous.

Pour établir cette clé secrète partagée, les échanges entre Alice et Bob ne sont pas chiffrés mais, même si un troisième participant (appelé Ève, malveillant) écoute tous les échanges il lui sera impossible de déterminer cette clé secrète.

Ce protocole d'échange de clés de Diffie-Hellmann est en réalité basé sur des concepts mathématiques qui dépassent le cadre du programme de Terminale NSI (un encart explique cela pour les plus curieux en-dessous). Pour comprendre le principe, une analogie est souvent faite avec des pots de peintures :

Illustration conceptuelle de l'échange de clef Diffie-Hellman
Crédit : Idée originale : A.J. Han VinckVersion vectorielle : FlugaalTraduction : Dereckson, Domaine public, via Wikimedia Commons

Étape 1 : Alice et Bob choisissent au préalable une peinture commune, ici le jaune. Cette couleur est connue de tous, y compris de l'intrus Ève.

Étape 2 : Alice choisit une autre couleur secrète (ici du rouge). Elle mélange la peinture commune et sa couleur secrète et obtient de l'orange. Alice envoie la couleur orange à Bob. La couleur orange est connue d'Ève.

Étape 3 : Bob fait de même : il choisit une couleur secrète (ici du cyan) qu'il mélange à la peinture commune et il obtient du bleu. Bob envoie sa couleur bleu à Alice. La couleur bleue est connue d'Ève.

Étape 4 : Alice prend la couleur reçue (le bleu) qu'elle mélange avec sa couleur secrète rouge. Elle obtient une couleur brune.

Étape 5 : Bob prend la couleur reçue (le orange) qu'il mélange avec sa couleur secrète cyan. Il obtient la même couleur brune.

À l'issue du protocole, Alice et Bob possèdent la même couleur brune qui représente la couleur secrète partagée. La sécurité du protocole réside dans le fait qu'il est difficile pour Ève d'extraire les couleurs secrètes (rouge et cyan) à partir des couleurs publiques (orange et bleue) même en connaissant la couleur commune de départ (jaune) : elle ne peut donc pas trouver la couleur brune secrète. L'analogie fonctionne car :

• si on connait une couleur $x$ et la couleur du mélange $M(x,y)$ entre les couleurs $x$ et $y$, il est « difficile » de déterminer exactement la nuance de couleur $y$
• le mélange de trois couleurs donne la même couleur peut importe l'ordre dans lequel on fait le mélange : $M(M(x,y),z) = M(M(x,z),y)$.

Une fois que la clé secrète partagée (la couleur commune) est connue d'Alice et Bob, ils peuvent l'utiliser de manière symétrique pour chiffrer et déchiffrer leurs communications de manière sûre.

Concrètement, ce ne sont pas des couleurs qu'Alice et Bob choisissent mais un nombre premier et des entiers, tous très grands, et des calculs sur ces nombres permettent de faire les « mélanges » pour obtenir d'autres nombres à partir desquels il est très compliqué de retrouver les nombres de départ. Pour en savoir plus sur la théorie mathématique derrière l'échange de clés de Diffie-Hellmann, consultez les sections Principe orginial et Exemple de l'article Wikipédia : Diffie-Hellmann.

Des variantes existent, basées sur d'autres problèmes mathématiques, encore plus difficiles à inverser.

Le protocole d'échange de clés de Diffie-Hellmann possède en revanche un point faible : il ne permet pas d'authentifier les participants. Autrement dit, Ève pourrait se faire passer pour Bob auprès d'Alice, et aurait donc accès à la clé secrète, on parle d'attaque de l'homme au milieu, ou man in the middle en anglais (voir plus bas).

D'autres chiffrements asymétriques, comme le chiffrement RSA, règlent ce problème d'authentification.

RSA

Diffie et Hellmann ont proposé en 1976 un protocole théorique de chiffrement asymétrique, basé sur l'utilisation d'un couple de clés : une clé publique et une clé privée notées respectivement $C^{\text{pub}}$ et $C^{\text{priv}}$. L'une permet de chiffrer le message $m$ et l'autre permet de le déchiffrer.

La façon dont sont générées les clés est complexe et repose sur des théorèmes d'arithmétique bien connus, comme le petit théorème de Fermat étudié en option mathématiques expertes. Retenez que les deux clés sont liées de la façon suivante :

• $C^{\text{pub}}(C^{\text{priv}}(m)) = C^{\text{priv}}(C^{\text{pub}}(m)) = m$
• connaissant $C^{\text{pub}}$ il est impossible de trouver $C^{\text{priv}}$ et réciproquement
• il est impossible de trouver $m$ en connaissant $C^{\text{pub}}(m)$ ou $C^{\text{priv}}(m)$

En utilisant ces deux clés, Alice va pouvoir envoyer un message à Bob de manière chiffrée :

Étape 1 : Bob fabrique deux clés :

• sa clé publique $C^\text{pub}_\text{Bob}$, qu'il envoie à Alice,
• et sa clé privée $C^{\text{priv}}_\text{Bob}$, qu'il ne divulgue à personne.

Étape 2 : Alice utilise la clé publique de Bob pour chiffrer son message $m$ puis envoie ce message $C^{\text{pub}}_\text{Bob}(m)$ à Bob.

Étape 3 : Bob utilise sa clé privée pour déchiffrer le message d'Alice : $C^\text{priv}_\text{Bob}(C^\text{pub}_\text{Bob}(m))=m$.

Ainsi, si Ève intercepte le message d'Alice à l'étape 2, elle ne pourra rien en faire car elle ne connaît pas la clé privée de Bob : la communication est donc sécurisée.

Vous remarquerez que si Bob veut communiquer avec Alice, il suffit à cette dernière de générer une clé publique et une clé privée, et Bob n'a plus qu'à utiliser la clé publique d'Alice pour chiffrer ses messages et seule Alice pourra les déchiffrer avec sa clé privée.

C'est en 1978, que Ronald Rivest, Adi Shamir et Leonard Adleman, travaillant alors au MIT, ont proposé un algorithme portant leurs initiales, RSA, permettant d'implémenter concrètement ce principe de chiffrement asymétrique.

Pour la petite histoire, Rivest, Shamir et Adleman voulaient démontrer qu'il était impossible de trouver un algorithme implémentant le protocole décrit ci-dessus. Ils ont donc démontré l'inverse de ce qu'ils souhaitaient au départ. En réalité, c'est le mathématicien et cryptographe britannique Clifford Cocks qui aurait découvert "RSA" trois ans auparavant mais son travail était classé secret et n'a été rendu public qu'en 1997.

En réalité, le chiffrement RSA demande des calculs assez lourds pour chiffrer et déchiffrer des messages. Ces calculs ralentissent les échanges, ce qui le rend en pratique difficilement utilisable lorsque les données à échanger sont volumineuses (par exemple, de la vidéo en temps réel). Mais on peut très bien l'utiliser avec le même objectif que l'échange de clé de Diffie-Hellmann : on utilise RSA pour s'échanger une clé symétrique de manière sûre et ensuite le reste des communications peut se poursuivre avec un chiffrement symétrique beaucoup plus efficace, comme AES. Pour cela, à l'étape 2 précédente, Bob choisit une clé symétrique (AES) et la chiffre avec la clé publique d'Alice. Il lui transmet ainsi de manière sécurisée cette clé et Alice la déchiffre à l'étape 3 avec sa clé privée. Alice et Bob ont alors à disposition une clé symétrique leur permettant de poursuivre les échanges avec un chiffrement symétrique.

Authentification

Le chiffrement RSA est l'un des plus utilisé actuellement car, en plus d'assurer des communications sécurisées, il permet également de gérer l'authentification des participants.

Attaque man in the middle

Le protocole d'échange de clés de Diffie-Hellmann, ainsi que la version présentée de RSA dans le paragraphe précédent ne permettent pas d'être sûr de l'identité des participants à la communication.

En effet, si Ève est malveillante, elle peut se faire passer pour Bob auprès d'Alice (et aussi pour Alice auprès de Bob si elle le souhaite). Il existe plusieurs manières pour un attaquant de se faire passer pour l'un des correspondants (phishing, imposture ARP, DNS Poisoning, analyse de traffic, déni de service, etc.) mais nous n'en parlerons pas ici.

On se retrouve alors dans la situation où Ève se situe entre Alice et Bob et aucun des deux ne peut savoir que le canal de communication a été compromis. On parle d'attaque de l'homme au milieu.

Une façon de contourner ce problème s'appelle l'authentification qui assure que chacun s'adresse à la bonne personne.

Certificats et autorités de certification

Pour prouver son identité, un participant présente ce qu'on appelle un certificat qui est délivré par une autorité de certification, qui est une entité en laquelle tous les participants font confiance (en pratique ce sont des entreprises spécialisées, des états, des associations à but non lucratif). Ces tiers de confiance produisent des certificats numériques à partir des clés RSA publiques et privées des participants de la manière suivante :

Étape 1 : Bob demande un certificat à une autorité de certification (AC), qui :

• vérifie qu'il s'agit bien de Bob (on ne détaille pas ici les manières de procéder)
• chiffre la clé publique de Bob avec sa clé privée : $s = C^{\text{priv}}_{\text{AC}}(C^{\text{pub}}_\text{Bob})$

Le fichier $s$ obtenu s'appelle le certificat, que Bob peut communiquer à ses interlocuteurs pour justifier qu'il s'agit bien de lui.

Étape 2 : Alice veut communiquer avec Bob, elle le contacte et Bob lui fourni :

• sa clé publique $C^{\text{pub}}_\text{Bob}$
• le certificat $s$

Étape 3 : Alice récupère la clé publique de AC, en qui elle a aussi confiance, et l'applique au certificat : $$C^{\text{pub}}_\text{AC}(s)=\underbrace{C^{\text{pub}}_\text{AC}(C^{\text{priv}}_\text{AC}}_{\text{s'annulent}}(C^{\text{pub}}_\text{Bob}))=C^{\text{pub}}_\text{Bob}$$

Si le résultat du calcul précédent correspond à la clé publique que Bob lui a transmise, alors Alice est certaine que Bob est bien l'expéditeur du message précédent.

Étape 4 : Alice peut alors initialiser la communication avec Bob en chiffrant une clé symétrique avec la clé publique de Bob ou en utilisant le protocole de Diffie-Hellmann pour se mettre d'accord sur une clé partagée.

Lorsque l'autorité de certification chiffre la clé publique de Bob avec sa clé privée, on dit qu'elle signe la clé publique de Bob, d'où le nom $s$. Ce mécanisme est aussi utilisé pour les signatures électroniques.

Le protocole HTTPS

On a vu en classe de Première le fonctionnement du protocole HTTP utilisé sur le Web pour communiquer. Ce protocole historique a deux défauts :

• les informations transitent en clair sur le réseau et donc peuvent être lues par un tiers.
• il est vulnérable à l'attaque de l'homme au milieu

Pour chiffrer les échanges et authentifier les participants sur le Web, c'est le protocole HTTPS qui est utilisé (pour Hypertext Transfer Protocol Secure). Il s'agit du protocole HTTP auquel on a ajouté une couche de cryptographie grâce au protocole TLS (Transport Layer Security, sécurité de la couche de transport), anciennement appelé SSL (Secure Sockets Layer, couche de sockets sécurisée).

Le protocole TLS permet initialement d'authentifier le serveur et de mettre en place une clé de chiffrement symétrique, appelée clé de session. Les échanges peuvent ensuite se poursuivre suivant le protocole HTTP en chiffrant les messages avec la clé de session :

Fonctionnement du protocole HTTPS

Étape 1 : Le client envoie un message (appelé Hello) au serveur pour demander une connexion sécurisée (il indique aussi les algorithmes cryptographiques qu'il peut utiliser)

Étape 2 : Le serveur envoie sa réponse contenant notamment sa clé publique et son certificat qui n'est autre que la signature de la clé publique par l'autorité de certification.

Étape 3 : Le client fait appel à l'autorité de certification pour vérifier le certificat grâce à la clé publique de l'autorité de certification (en pratique, les navigateurs disposent des clés publiques des autorités de certification) comme indiqué dans le paragraphe précédent.

Étape 4 : Une fois le certificat validé, le client et le serveur utilisent un algorithme de chiffrement à clé publique (asymétrique) pour définir une clé de chiffrement partagée appelée clé de session :

• soit RSA : le client choisit une clé et la chiffre avec la clé publique du serveur avant de l'envoyer au serveur
• soit l'échange de la clé se fait selon l'algorithme de Diffie-Hellmann

Étape 5 : Le client et le serveur utilisent cette clé de session dans un chiffrement symétrique (par exemple AES), beaucoup plus rapide, pour poursuivre les échanges avec le protocole HTTP mais dans lequel les requêtes et les réponses sont chiffrées.

Le port utilisé pour se connecter via HTTPS à un serveur est le port 443, différent du port 80 réservé au protocole HTTP.

Si le serveur souhaite une authentification du client, celle-ci est généralement faite par un mécanisme d'identifiant et de mot de passe pour se connecter.

Dans le navigateur

Si la certification échoue à l'étape 3, alors le navigateur alerte l'utilisateur avec un écran similaire à celui-ci :

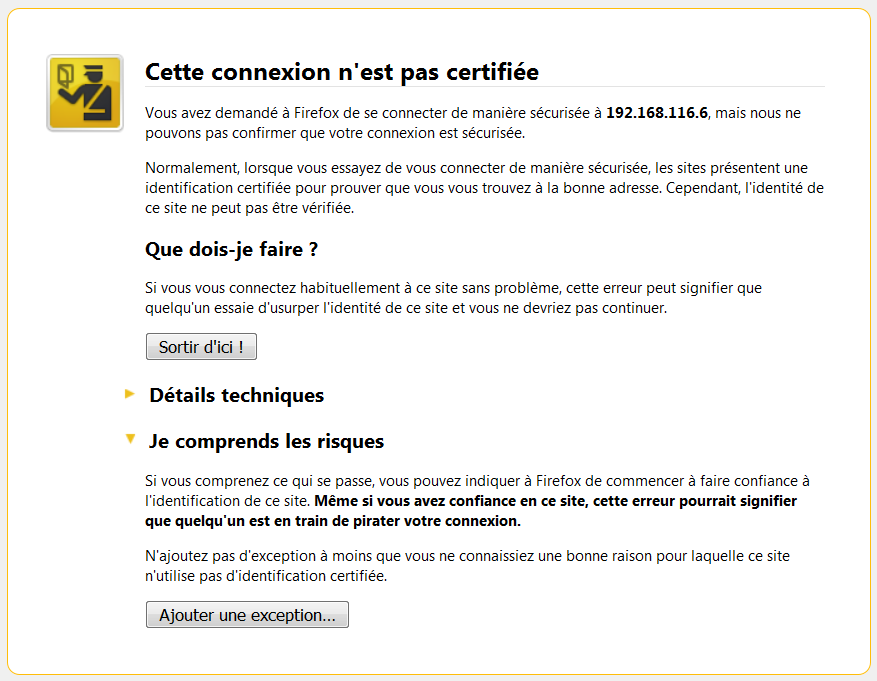
Crédit : Cepheus, Domaine public, via Wikimedia Commons

De plus, toujours à l'étape 3, le client vérifie également que le certificat est toujours valide. Si ce n'est pas le cas, le navigateur prévient l'utilisateur de l'expiration du certificat (le serveur est néanmoins authentifié) et on obtient des avertissements qui ressemblent à ceci :

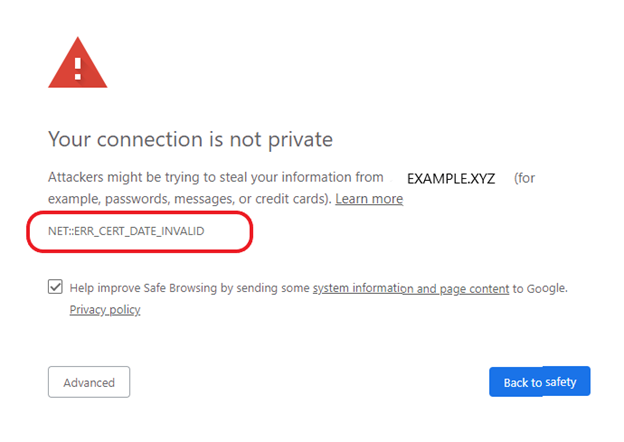
Enfin, sachez qu'il est possible de consulter le certificat d'un serveur (auquel on est connecté en HTTPS) dans le navigateur en cliquant sur le cadenas situé à côté de la barre d'URL. Par exemple, si on cherche le certificat du site stjonum.fr, le navigateur affiche cela :

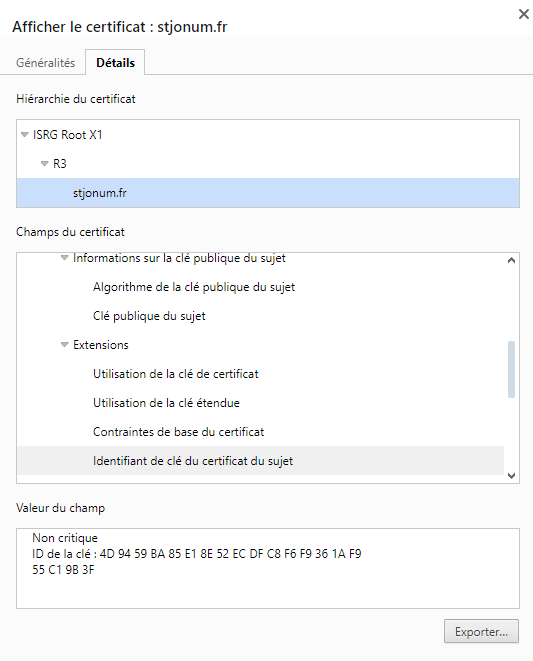
On peut ainsi voir l'authorité qui certifie la connexion et comment la connexion a été chiffrée dans les détails techniques :

Le protocole utilisé

L'authentification est assuré par le protocole RSA.

Les diférentes clés...

Bilan

• Il existe deux familles de chiffrement : le chiffrement symétrique et le chiffrement asymétrique.
• Dans le cas d'un chiffrement symétrique, les deux participants utilisent une clé partagée qui sert à la fois à chiffrer et à déchiffrer les messages. Un des algorithmes de chiffrement symétrique le plus utilisé actuellement est AES.
• Cette clé doit absolument restée privée car sa connaissance par un tiers lui permettrait de déchiffrer toutes les communications. Les chiffrements symétriques ont un point faible : il n'est pas possible de s'échanger cette clé partagée de manière sûre car le canal n'est pas encore sécurisé.
• C'est pourquoi des chiffrements asymétriques ont vu le jour. On parle aussi de chiffrements à clé publique car les algorithmes asymétriques sont basés sur des clés publiques et des clés privées utilisées pour :
  • s'échanger de manière sécurisée une clé partagée (algorithme de Diffie-Hellmann),
  • chiffrer et déchiffrer directement les communications (algorithme RSA).
• L'échange de clés de Diffie-Hellmann est vulnérable à l'attaque de l'homme au milieu car il ne permet pas d'authentifier les participants. En revanche, RSA permet de gérer l'authentificaiton grâce à des autorités de certification qui signent des certificats attestant de l'identité d'un participant.
• Un algorithme de chiffrement asymétrique est plus lent car gourmand en calculs, c'est pourquoi on l'utilisera surtout pour sécuriser le début d'une communication, afin d'échanger une clé symétrique de manière sûre, avant d'utiliser cette clé pour poursuivre les échanges avec un algorithme de chiffrement symétrique, comme c'est le cas du protocole HTTPS
• Le protocole HTTPS, utilisé pour sécuriser les communications sur le Web, ajoute une couche de sécurité au protocole HTTP grâce au protocole TLS (anciennement SSL). TLS utilise RSA au départ pour sécuriser la communication et authentifier le serveur. Ensuite, un échange de clé peut avoir lieu, grâce à Diffie-Hellmann ou RSA, permettant aux deux participants de disposer d'une clé symétrique, appelée clé de session, qui servira à poursuivre les échanges (réponses/requêtes HTTP) avec un chiffrement symétrique, plus rapide, tel que AES.
• Tous les algorithmes de chiffrement actuels reposent sur des clés, que l'on allonge au fur et à mesure que les performances des ordinateurs augmentent pour prévenir à des attaques de type force brute. Il est important de noter que tous les chiffrements actuels deviendraient immédiatement obsolètes si un ordinateur quantique voit le jour !

---

Références :

• Articles Wikipédia : Cryptographie symétrique, Cryptographie asymétrique, Échange de clés de Diffie-Hellmann, Chiffrement RSA, Attaque de l'homme du milieu, Transporte Layer Security, masque jetable, Advanced Encryption Standard
• Livre Numérique et Sciences Informatiques, 24 leçons, Terminale, T. BALABONSKI, S. CONCHON, J.-C. FILLIATRE, K. NGUYEN, éditions ELLIPSES.
• Livre Prépabac NSI, Terminale, G. CONNAN, V. PETROV, G. ROZSAVOLGYI, L. SIGNAC, éditions HATIER.
• Les schémas ont été réalisés avec des images libres de droit (uniquement Public Domain ou CC0) accessibles sur le site : https://www.svgrepo.com/.

---

Inspiré du site de Germain Becker.