Parcours d'un arbre
On décide de prendre l'implémentation des arbres donnés ci-dessous :
class Arbre:
def __init__(self,valeur):
self.v=valeur
self.fg=None
self.fd=None
def ajout_gauche(self,val):
self.fg=Arbre(val)
def ajout_droit(self,val):
self.fd=Arbre(val)
def affiche(self):
"""permet d'afficher un arbre"""
if self==None:
return None
else :
return [self.v,Arbre.affiche(self.fg),Arbre.affiche(self.fd)]
def taille(self):
if self==None:
return 0
else :
return 1+Arbre.taille(self.fg)+Arbre.taille(self.fd)
def hauteur(self):
if self==None:
return 0
elif self.fg==None and self.fd==None:
return 0
else :
return 1+max(Arbre.hauteur(self.fg),Arbre.hauteur(self.fd))
def get_valeur(self):
if self==None:
return None
else:
return print(self.v)
Prise en main de l'implémentation
-
Implémenter cet arbre :
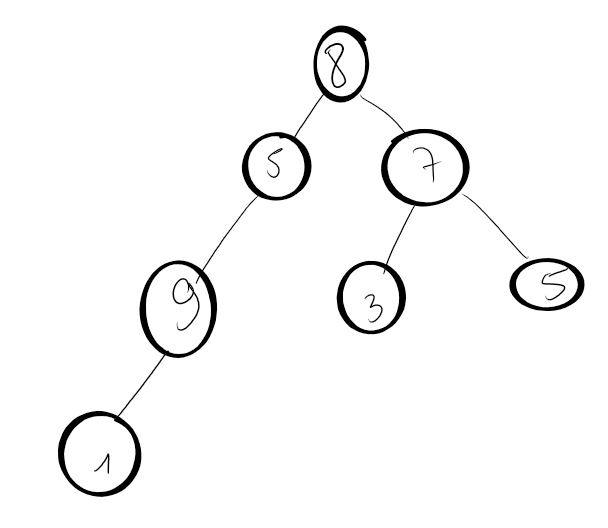
- Tester les différentes méthodes sur cet arbre.
Parcours en profondeur : infixe, préfixe et suffixe
Dans cette partie, nous allons aborder les parcours en profondeur. Il existe trois manières de parcourir un arbre en profondeur comme nous allons le voir. L'idée de ces parcours, c'est de descendre tout en bas de l'arbre avant de se déplacer vers la droite de l'arbre.
Ces parcours sont parfois notés DPS pour Depth-First Search.
Ces parcours serviront à réaliser des algorithme de recherche textuelle par exemple ou à gérer des "AI" de jeux vidéos.
Parcours préfixe
Dans ce parcours on note tous les nœuds en commençant par la racine puis les deux sous arbres.
Réaliser à la main le parcours préfixe de cet arbre :
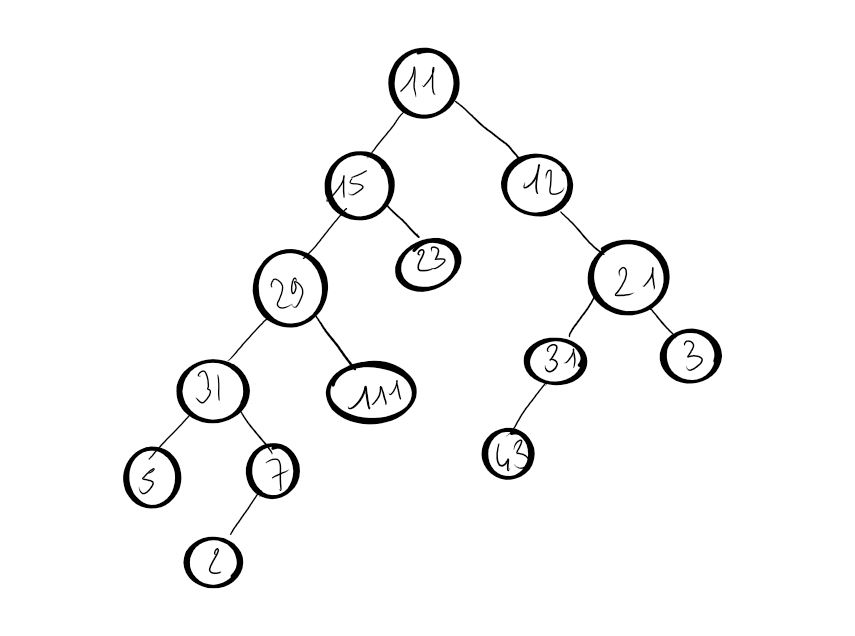
Algorithme du parcours préfixe.
voila la méthode écrite en Python du parcours préfixe d'un arbre de recherche:
def dfs_prefixe(self):
if self==None:
return None
else :
Arbre.get_valeur(self)
Arbre.dfs_prefixe(self.fg)
Arbre.dfs_prefixe(self.fd)
Parcours infixe
Dans ce parcours on note tous les nœuds en commençant par le sous arbre gauche puis la racine puis le sous arbre droit.
Réaliser à la main le parcours infixe de cet arbre :

Ecrire l'algorithme du parcours infixe.
Parcours suffixe
Dans ce parcours on note tous les nœuds en commençant par le sous arbre gauche puis le sous arbre droit et enfin la racine .
Réaliser à la main le parcours suffixe de cet arbre :

Ecrire l'algorithme du parcours suffixe.
Parcours en largeur d'abord
Dans cette partie, nous allons aborder les parcours en largeur.
Ce parcours est parfois noté BPS pour Breadth-First Search.
Parcours en largeur
Quand on parcourt en largeur un arbre, on note chaque sommet niveau par niveau et en commençant par la gauche.
le parcours en largeur de cet arbre :

est : 8-5-7-9-3-5-1
On reprend l'implémentation de file
class Element:
#chaque élément a pour attribut : le precedent , le suivant et la valeur de l'élément
def __init__(self,x):
self.val=x
self.precedent=None
self.suivant=None
def __str__(self): #methode qui permet de lance un print sur un tel objet
return str(self.val)+"-"+str(self.suivant)l'objet file :
class File:
#ici une file est la donnée de deux attributs : la file complète de type Element et le dernier élément de la file de type Element
def __init__(self):
self.tete=None
self.queue=None
def enfile(self,x):
e=Element(x) #on transforme l'élément à ajouter en un objet Element de listes doublement Chainées
if self.tete==None:
self.tete=e #file vide la tete est remplacée par l'élément e
else:
e.precedent=self.queue #le précédent de l'élément pointe sur l'ancienne queue de la file
self.queue.suivant=e #l'ancienne queue de la file pointe sur e avec suivant
self.queue=e #on redéfinit self.queue par e.
def file_vide(self):
return self.tete is None #renvoie True si None et False sinon
def defile(self):
if not self.file_vide():
e=self.tete #on stocke l'élément à defiler
if e.suivant is None: #cas où il n'y a qu'un élément
self.tete=None
self.queue=None
else:
self.tete=e.suivant
self.tete.precedent=None
return e.val
def __str__(self):
return str(self.tete)Algorithme BFT
def BFT(arbre):
f=File()
f.enfile(arbre)
l=[]
while not f.file_vide():
a=f.defile()
l.append(a.v)
if a.fg!=None:
f.enfile(a.fg)
if a.fd!=None:
f.enfile(a.fd)
return lTester l'algorithme sur cet arbre :

Algorithmes des arbres binaires de recherche
Un arbre binaire de recherche (ABR) est un arbre binaire dans lequel chaque nœud possède une clé, telle que chaque nœud du sous-arbre gauche ait une clé inférieure ou égale à celle du nœud considéré, et que chaque nœud du sous-arbre droit possède une clé supérieure ou égale à celle-ci — selon la mise en œuvre de l'ABR, on pourra interdire ou non des clés de valeur égale. Un arbre binaire de recherche permet des opérations rapides pour rechercher une clé, insérer ou supprimer une clé.
Insertion
L'insertion d'un nœud commence par une recherche : on cherche la clé du nœud à insérer ; lorsqu'on arrive à une feuille, on ajoute le nœud comme fils de la feuille en comparant sa clé à celle de la feuille : si elle est inférieure, le nouveau nœud sera à gauche ; sinon il sera à droite. On choisit d’implémenter de tels arbres binaires à l’aide de la classe suivante, où on utilise des valeurs par défaut dans le constructeur pour les deux enfants :voici l'implémentation de l'arbre binaire de recherche
class ABR:
def __init__(self, cle : int, fg=None, fd=None):
self.__cle = int(cle)
self.__fg = fg # None ou un arbre de la classe ABR
self.__fd = fd # None ou un arbre de la classe ABR
def __repr__(self):
if self.feuille():
return "<" + str(self.__cle) + ">"
fg = "<>" if self.__fg is None else self.__fg.__repr__()
fd = "<>" if self.__fd is None else self.__fd.__repr__()
return "<{0},{1},{2}>".format(self.__cle, fg, fd)
def feuille(self) -> bool:
""" retourne True si le noeud est une feuille, False sinon """
return self.__fg == None and self.__fd == None
def infix_parcours(self, sep=" "):
""" traitement du nœud entre les deux sous-arbres """
s = ""
if self.__fg is not None:
s += self.__fg.infix_parcours(sep)
s += str(self.__cle) + sep
if self.__fd is not None:
s += self.__fd.infix_parcours(sep)
return s
def insert(self, cle : int):
"""
insertion d'une clef dans un ABR
si la clef est < clef du noeud, on insère à gauche du noeud
sinon on insère à la droite du noeud
Arguments:
cle -- clef de l'arbre
"""
def __insert(noeud : object, cle : int):
if cle < noeud.__cle:
if noeud.__fg is not None:
__insert(noeud.__fg, cle)
else:
noeud.__fg = ABR(cle)
elif cle > noeud.__cle:
if noeud.__fd is not None:
__insert(noeud.__fd, cle)
else:
noeud.__fd = ABR(cle)
__insert(self, cle)
def recherche(self, cle ):
"""
recherche d'une clef dans un ABR
Arguments:
cle -- clef recherchée
Retour:
True si la clef est présente, False sinon
"""
def __recherche(noeud : object, cle):
if noeud == None:
return False
if cle < noeud.__cle:
return __recherche(noeud.__fg, cle)
elif cle > noeud.__cle:
return __recherche(noeud.__fd, cle)
else:
return True
return __recherche(self, cle)
Implémenter l'arbre suivant : (pour le visualiser, utiliser print())
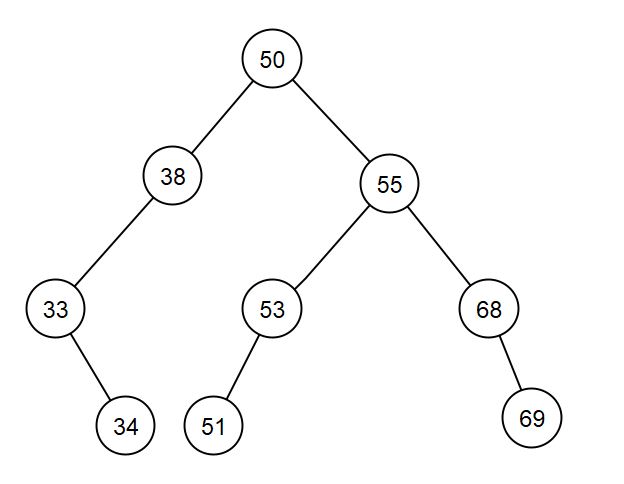
Recherche d'une clé
Ecrire la méthode recherche(self,val) qui renvoie True si val est une clé de l'arbre et False sinon.
Le principe ici est celui de la dichotomie. On élimine grâce à la structure des arbres binaires de recherche la moitié des nœuds restant à chaque étape.
Insérer une clé
La méthode qui insère un élément dans un arbre binaire de recherche est déjà écrite.
Commenter cette méthode.
Exercices
Ecrire une méthode min(self) qui renvoie la clé minimale d'un arbre.
Ecrire une méthode max(self) qui renvoie la clé maximale d'un arbre.