SNT

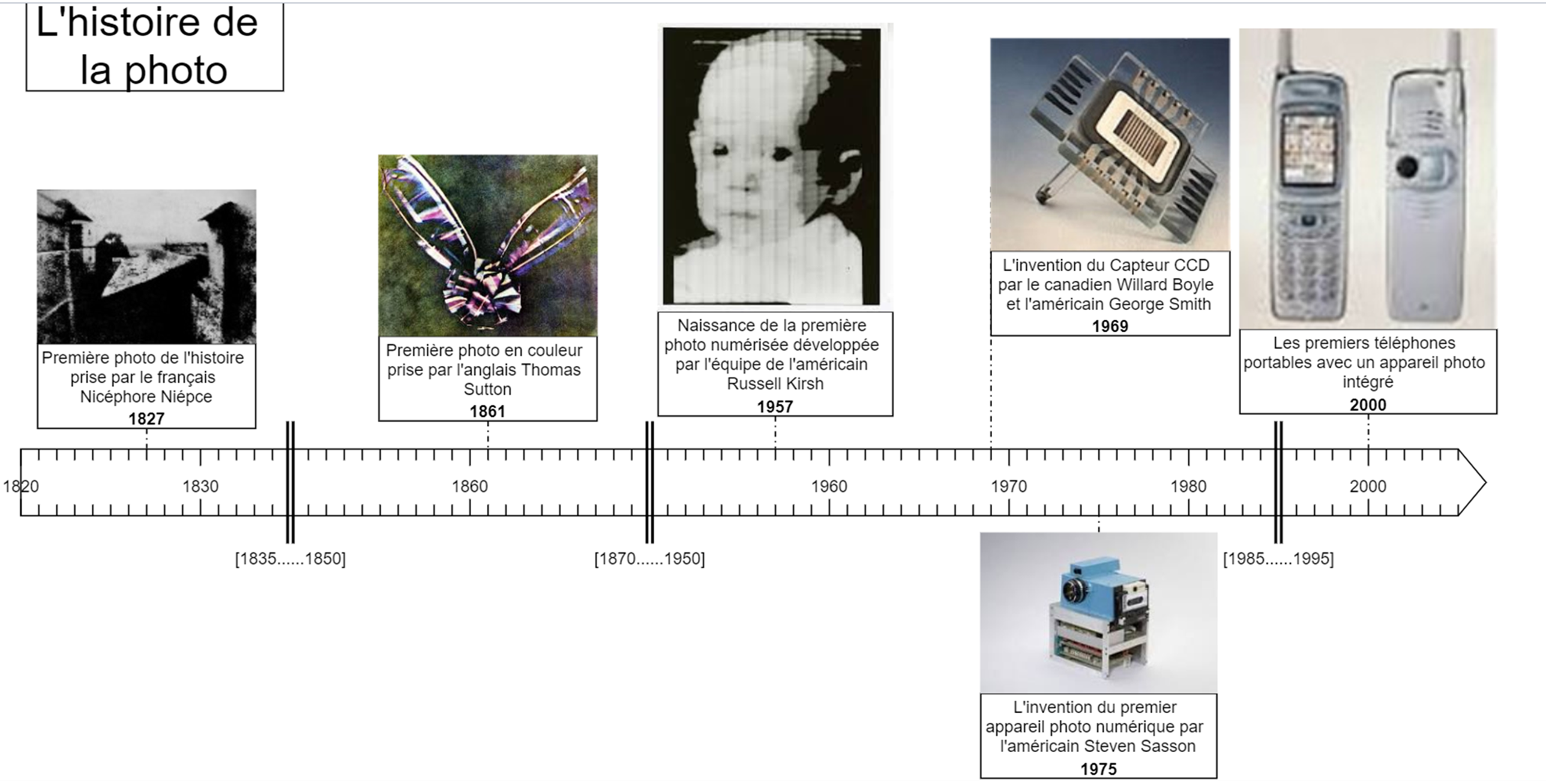
Ci-dessus quelques repères historiques de la photo numérique présentés sous la forme d'une frise :

Partie 1 : L'oeil et le capteur numérique

L'oeil et le capteur photographique

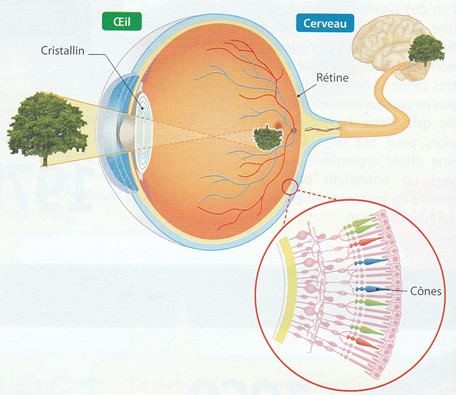
1.1.1 La vision humaine Les rayons lumineux provenant d'un objet sont projetés au fond de l'oeil sur la rétine. Celle-ci comprend des cellules sensibles à la lumière : les cônes. certains cônes perçoivent la couleur rouge, d'autres la couleur verte et d'autres la couleur bleue. Les cônes sensibles au vert sont les plus présents chez l'être humain. Ils transforment l'énergie lumineuse en impulsion électrique. Cette impulsion est transmise au cerveau par l'intermédiaire du nerf optique. La couleur est ensuite reconstituée par le cerveau par addition du rouge, du vert et du bleu.
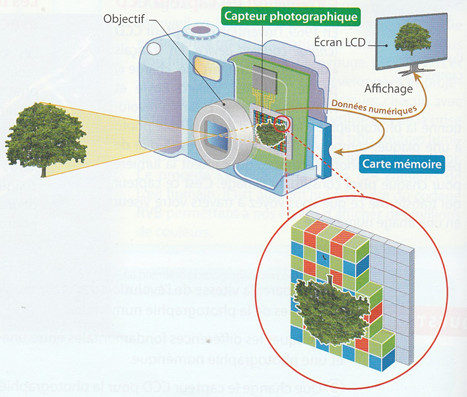
1.1.2 L'appareil photo numérique Les rayons lumineux provenant d'un objet sont projetés dans l'appareil photo sur le capteur photographique. Celui-ci est constitué de cellules sensibles à la lumière. La mesure de l'intensité lumineuse est transformée en données numériques puis stockée dans la mémoire de l'appareil.
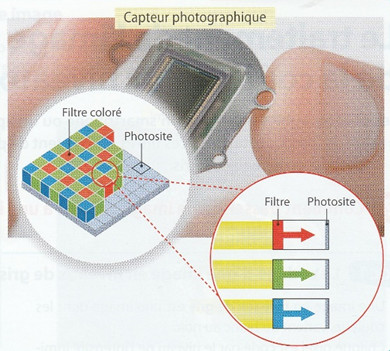
1.1.3 Le fonctionnement du capteur photographique Les capteurs photographiques sont des éléments électroniques sensibles à la lumière, qui produisent des électrons (de l'électricité) lorsqu'ils reçoivent des photons (de la lumière). Un capteur d'appareil photo numérique est composé de cellules photosensibles : les photosites. Pour que ceux-ci distinguent les couleurs, chacun est placé derrière un filtre qui ne laisse passer que les rayons d'une seul couleur : rouge, vert ou bleu (2 verts, 1 rouge et un bleu par carré). Les photosites mesurent ainsi l'intensité lumineuse des rayons rouges (R), des rayons verts (V) et des rayons bleus (B). La tension électrique produite est ensuite convertie en nombre et envoyée au processeur de l'appareil photo. La définition d'un capteur est le nombre total de ses photosites.
Source des images : SNT 2^de, Sciences numériques et Technologie, pages 106-107, édition Delagrave, Paris 2019.

En comparant les images schématisant la vision humaine et l'appareil photo numérique, quel est l'équivalent au niveau de l'appareil numérique :
1. du cristallin de l'oeil humain ?
2. de la rétine de l'oeil ?
3. du cerveau humain ?
4. d'un cône ?
Où se situe le capteur d'un appareil photo ?
Pourquoi mettre sur un capteur photographique deux fois plus de photosites sensibles à la couleur verte qu'aux deux autres couleurs ?
Que représente la définition d'un capteur photo ?
Quels sont les principaux éléments d'un appareils photos ? Résumer son principe de fonctionnement.

Notion d'image numérique

Une image numérique est constituée d’un ensemble de pixels, c’est-à-dire de petits carrés colorés disposés les uns à côté des autres sous la forme d'un tableau à deux dimensions, le pixel représente ainsi le plus petit élément constitutif d'une image numérique.
Chaque pixel est caractérisé par sa position sur l’image (sous forme de coordonnées), et sa couleur.

Définition d'une image

La définition d’une image numérique est le nombre de pixels qui la composent.

si par exemple les dimensions de l’image sont 300 pixels en largeur et 200 pixels en hauteur, sa définition sera de 60 000 pixels ($60 000 = 200\times 300$).

On parle aussi de définition lorsqu’on veut exprimer la qualité d’un appareil photographique : si un fabricant annonce que son appareil a 18 mégapixels (soit 18 millions de pixels), cela signifie qu’il prend des photographies dont les dimensions sont $5184 \times 3456$ pixels.
Cependant en pratique, il est bien difficile de distinguer une photo à 18 mégapixels d’une autre à 12 mégapixels.

Résolution d'une image

La résolution d’une image est exprimée par un nombre de pixels par unité de longueur (souvent le pouce, soit 2,54 centimètres).

Il est utile de l’évoquer lorsqu’on affiche une image sur un écran ou qu’on l’imprime sur papier : habituellement, les écrans d’ordinateurs ont une résolution de 72 pixels/pouce (soit environ 28 pixels/centimètre), alors que les impressions sur papier requièrent une résolution de 300 pixels/pouce.

On dispose d’une image de dimensions 75×50 pixels, et on l’imprime sur une feuille de dimensions 15×10 centimètres. Quelle sera la taille de chaque pixel imprimé ? Que peut-on craindre du résultat ?
Quelles devraient être les dimensions de la feuille si on souhaite réaliser une impression avec une résolution de 100 pixels/pouce?
On souhaite imprimer une image sur une feuille de dimensions 15×10 centimètres. Quelles devraient être les dimensions de l’image (en pixels) si on souhaite obtenir une résolution de 300 pixels par pouce ?

Profondeur de couleur

La profondeur de couleurs, dont l'unité est le "bits par pixel" (bpp), correspond au nombre de bits (c'est-à-dire de 0 et de 1) nécessaire pour stocker en mémoire la couleur d'un pixel.
Plus la profondeur de couleurs est grande plus l'échelle de nuances des couleurs est grande et plus la qualité de l'image est meilleure.

Voici la même photographie a été stockée en tant que trois images ayant une profondeur de couleurs différents :

l'une a été enregistrée avec 4 bpp, c'est à dire avec seulement 16 couleurs possibles,
une autre avec 8 bpp, c'est à dire avec 256 couleurs possibles,
enfin la dernière avec 24 bpp, c'est à dire avec environ 16 millions de couleurs possibles.

Image 1 :
Image 2 :
Image 3 :

Associer à chacune des images ci-dessus sa profondeur.

Vous pouvez regarder entre autre le centre de l'allée pour différencier certains cas.

Le poids d'une image

Le poids d'une image est la mémoire nécessaire à son enregistrement, il est mesuré en kilooctets, notés Ko, ou en mégaoctets, notés Mo.

Dans un appareil photo numérique, quel réglage permet d'obtenir des photos de meilleure qualité ?
Que représentent la définition du capteur et la définition d'une photo ? Le nombre de pixels de la photo est-il nécessairement égal au nombre de photosites du capteur ?
Comment évolue le poids d'une image si :
1. la définition de l'image augmente ?
2. la résolution de l'image augmente ?
3. la profondeur des couleurs de l'image augmente ?

Les métadonnées EXIF

Dans les appareils numériques, les métadonnées sont automatiquement inscrites et enregistrées dans le fichier image. L'ensemble de ces informations est appelé métadonnées EXIF, EXIF pour Exchangeable Image File Format (signification en français : "format d'échange de données pour les fichiers images" ).

Il est possible d’obtenir simplement les caractéristiques d’une image. Dans l’explorateur Windows, un clic droit sur le fichier image permet d’accéder à ses propriétés. Dans l’onglet Général, on trouve entre autres :

le nom du fichier ;
le type (ou format) du fichier (par exemple JPG) ;
son emplacement dans la mémoire de l’ordinateur ;
sa définition.

Dans l’onglet Détails, on trouve aussi :

ses dimensions;
sa résolution.
Les coordonnées GPS précises du lieu où a été prise l'image, etc ...

Téléchargez cette image en cliquant ici
Afficher les métadonnées EXIF de cette image en utilisant l'explorateur Windows.
Quelle est la définition de cette image ?
Quel est son poids ?
Quelles devraient être les dimensions de la feuille d'impression de cette image si on souhaite l'imprimer avec une résolution de 300 pixels/pouce ?
Quelle est la valeur de la profondeur en couleur de cette image ? Que signifie cette valeur ?
Déterminer les données permettant de déterminer la position du lieu où a été prise cette image.
A l'aide de ces données, déterminer le lieu où a été prise l'image.

Faire une recherche pour trouver un site qui permet de localiser un lieu à partir de ses coordonnées GPS.

Un internaute vient de publier sur une page Web deux photos :

Le but est de localiser le trésor !

Télécharger les deux images ci-dessous à l'aide d'un clic droit pour les mettre dans le même répertoire que celui de l'exercice précédent.
Etudier les métadonnées Exif disponibles sur la première photo. Quelles informations obtient-on sur l'image ?
Etudier les métadonnées Exif disponibles sur la seconde photo. Quelle information obtient-on sur le lieu où a été pris la photo ?
Outre les données directement accessibles depuis les propriétés du fichier image, d’autres métadonnées sont disponibles. Certains sites (ou logiciels) permettent d’extraire d’un fichier les métadonnées qu’il contient.
Par exemple, utiliser le site https://www.get-metadata.com/ pour extraire de nouvelles informations sur la localisation du trésor.
Localiser le lieu où le trésor est caché.

Pour protéger vos données personnelles, vous devez les supprimer avant de les envoyer ou de les publier sur un réseau social.

Pour chacune des images téléchargées de l'exercice précédent, ouvrir les propriétés de l'image et supprimer les propriétés et les informations personnelles par un clic judicieux.
Peut-on encore localiser le trésor à partir des données restantes ?

Pour effacer les métadonnées EXIF sur un smartphone, vous pouvez suivre les procédures proposées à cette adresse.

Les images proposées ci-dessus sont « libres de droits ».

Rechercher la signification de cette expression.

Si une image n’est pas « libre de droit », que peut-elle être ?

Pour les plus curieux

Si vous avez apprécié le fait d'essayer de localiser une photographie, sachez qu'il existe un collectif sur twitter qui propose d'apprendre aux utilisateurs de nouvelles techniques de vérification des images en ligne. Il suffit que les joueurs retrouvent l'endroit où a été pris la photo à partir d’indices présents dans la photo.
Attention ! Il ne suffit pas de se contenter de trouver des métadonnées dans ce jeu mais de repérer des indices visuels et d'effectuer des recherches sur Internet.

Chaque participant explique la démarche qui lui a permis de localiser la photo du jour : ainsi, au fil des résolutions, on apprend à trouver des indices et à les utiliser de manière performante !

Si vous voulez devenir des Sherlock Holmes du XXIè siècle, n'hésitez pas !

Comme de plus, de nombreux posts sont en anglais, vous vous améliorerez aussi dans la langue de Sherlock Holmes !

Voici une page web contenant une vidéo qui présente le jeu et explicite une résolution particulière. (vous y apprendrez en particulier comment faire pour retrouver une photo en taille originale pour pouvoir y trouver des indices.

Voici le lien pour accéder au collectif quiztime sur Twitter.